Question

Вычислить площадь фигуры ограниченной линиями

Answer 1

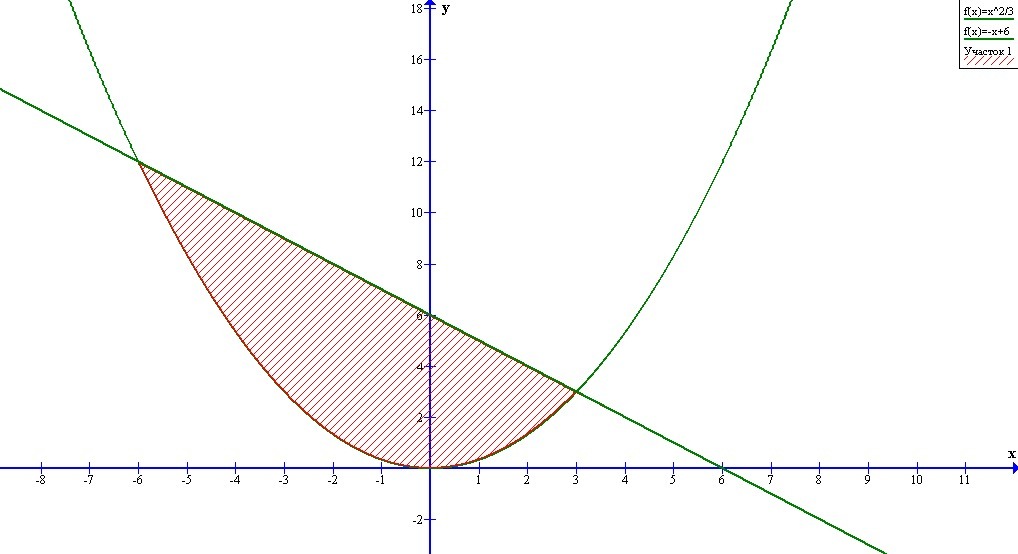
y = x²/3 - квадратичная функция. Графиком квадратичной функции является парабола, ветви которого направлены вверх

y = -x + 6 - прямая, проходящая через точки (0;6), (6;0)

Рабочая формула.  Если на отрезке [a;b] некоторая непрерывная функция f(x) больше либо равна некоторой непрерывной функции g(x), то площадь фигуры, ограниченной графиками данных функций и прямыми x=a, x=b, можно найти по формуле:

                                              $S=displaystyle intlimits^b_a {(f(x)-g(x))} , dx$

Найдем точки пересечения этих двух графиков, т.е.

$1/3x^2=-x+6\ \ x^2=-3x+18\ x^2+3x-18=0$

По т. Виета:  $x_1=-6$

                      $x_2=3$

Прямая у = -х + 6 расположена выше графика функции y = x²/3, значит

$S=displaystyle intlimits^3_{-6}bigg(-x+6-frac{x^2}{3}bigg)dx=bigg(-frac{x^2}{2}+6x-frac{x^3}{9}bigg)bigg|^3_{-6}=40.5$ кв. ед.