Постройте график функции у=х в -3 степени+3 а) Найдите наим. и наиб. значения функции на отрезке [1;2] б) Какая из точек А(1/2; 2 7/8) и В(1/2;11) принадлежит графику функции? в) Найдите точки пересечения графика данной функции с графиком функции у=х+3.
Ответы
Ответ дал:
0
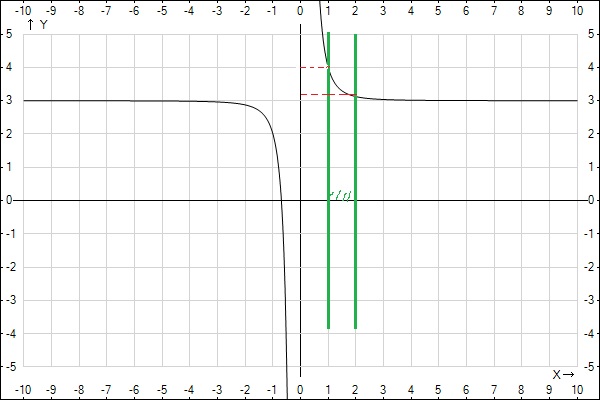
a)у(наим)= ; при х=2
у(наиб)=4 ; при х=1
б)Проверим точку A:
Значит точка A не принадлежит графику функции.
Проверим точку В:
Верно, значит точка В принадлежит графику функции.
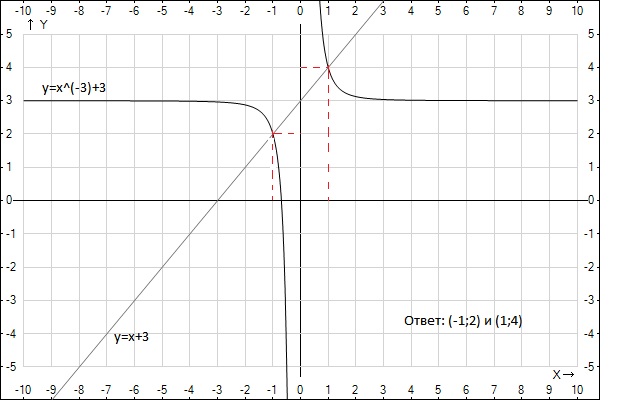
в)cмотри рисунок 2.
Приложения:
Вас заинтересует
2 года назад
8 лет назад
11 лет назад
11 лет назад
11 лет назад