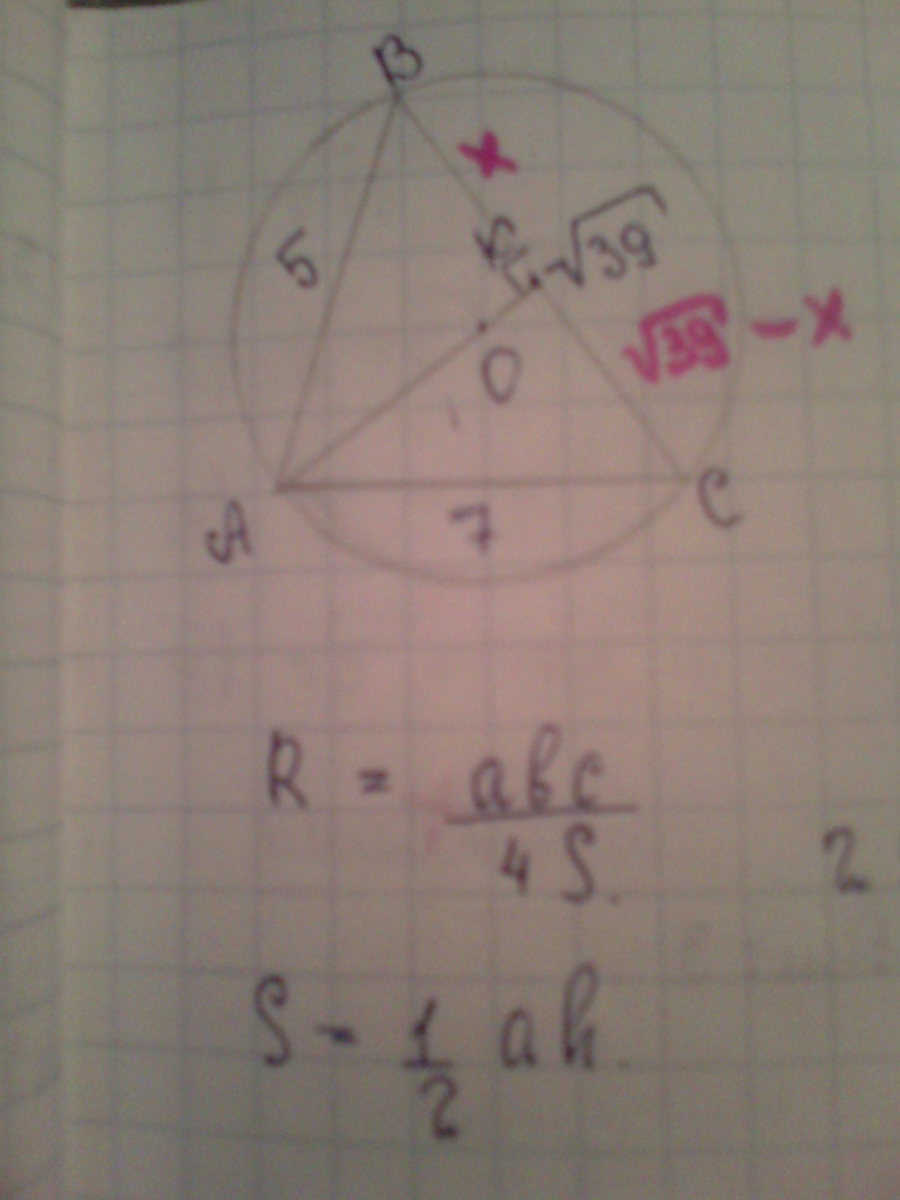
в треугольнике ABC известно, что AB =5, AC=7, и BC = √39. Найдите радиус описанной около этого треугольника окружности.
Нужен точный ответ!
Приложения:
vlada7899:
а это какой класс?
9 класс
опа....
Это к ОГЭ, в учебниках таких заданий нет
Ответы
Ответ дал:
3
5^2 + 7^2 - 2*5*7*cos(α) = 39;
cos(α) = 1/2; => sin(α) = √3/2;
2*R*sin(α) = √39;
R = √13;
Я не думаю, что хоть одна из этих выкладок нуждается в пояснении.
cos(α) = 1/2; => sin(α) = √3/2;
2*R*sin(α) = √39;
R = √13;
Я не думаю, что хоть одна из этих выкладок нуждается в пояснении.
всё нуждается в пояснении, потому что скоро ОГЭ, а я не понимаю геометрию. Поэтому это для меня лишь набор цифр. Вы можете разъяснить?
мне лично не понятно откуда вщяты косинус 1/2 и синус ....
ну первое выражение это по теореме косинусов , ладно ..... но дальше - откуда получен косинус 1/2, нет ни одного угла....
Я могу, но если вам не понятно, то дело плохо :) Первое соотношение - теорема косинусов, за α обозначен угол между сторонами 5 и 7; по найденному косинусу 1/2 ясно, что это угол 60°, синус которого √3/2; (вообще, всегда сумма квадратов синуса и косинуса угла равна 1) далее использовано следствие из теоремы синусов для треугольника 2*R*sin(α) = a; подробности - ищите в учебнике.
Чтобы "врубиться" в материал, лично Вам надо вывести 2*R*sin(α) = a; подсказка: это имеет отношение к вписанным углам.
как вы полусили косинус 1/2 между сторонами 5 и 7 ?
ну, как вам сказать :))) 25 + 49 - 70*cos(α) = 39; 70*cos(α) = 35;
спасибо. теорему косинусов я знаю, поменьше сарказма. а вот остальное решение меня сначало ввело в заблуждение, но я уже разобралась. Ещё раз спасибо.
ё моё, в формуле косинусов все члены были известны и только косинус угла Х , его то и нашли как в уравнении. Спасибо, поняла.
Вас заинтересует
2 года назад
2 года назад
7 лет назад
9 лет назад