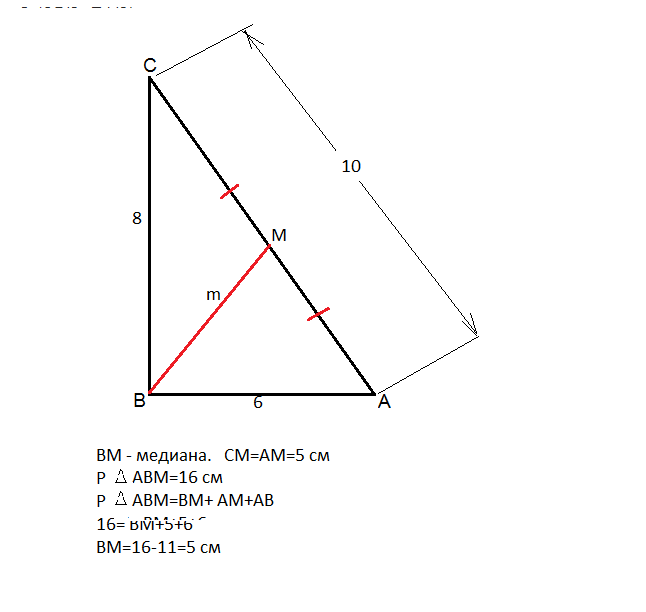
В треугольнике ABC проведена медиана BM. Известны стороны треугольника: AB=6 см, BC=8 см, AC=10 см. Найдите длину медианы если периметр треугольника ABM равен 16 см.
Ответы
Ответ дал:
7
Формула медианы треугольника
m=0,5*√(2а²+2b²-c²), где а и b- боковые стороны, с- сторона, к которой медиана проведена.
Произведя вычисления, получим длину медианы 5 см.
Но, обратив внимание на отношение сторон 6:8:10=3:4:5, увидим, что данный треугольник - египетский, следовательно, прямоугольный с прямым углом В, АС в нем - гипотенуза.
Медиана прямоугольного треугольника из прямого угла равна половине гипотенузы.
m=10:2=5 см
Проверка:
АВ+ВМ+МА=6+5+5=16 см ( периметр треугольника АВМ)
---------
Ещё один способ:
ВМ - медиана и делит сторону АС пополам.
СМ=АМ=10:2=5 ( см)
Р Δ АВМ=16 см
Р Δ АВМ=ВМ+АМ+АВ
16= ВМ+5+6
ВМ=16-11=5 ( см)
m=0,5*√(2а²+2b²-c²), где а и b- боковые стороны, с- сторона, к которой медиана проведена.
Произведя вычисления, получим длину медианы 5 см.
Но, обратив внимание на отношение сторон 6:8:10=3:4:5, увидим, что данный треугольник - египетский, следовательно, прямоугольный с прямым углом В, АС в нем - гипотенуза.
Медиана прямоугольного треугольника из прямого угла равна половине гипотенузы.
m=10:2=5 см
Проверка:
АВ+ВМ+МА=6+5+5=16 см ( периметр треугольника АВМ)
---------
Ещё один способ:
ВМ - медиана и делит сторону АС пополам.
СМ=АМ=10:2=5 ( см)
Р Δ АВМ=16 см
Р Δ АВМ=ВМ+АМ+АВ
16= ВМ+5+6
ВМ=16-11=5 ( см)
Приложения:
ЗлАяКаЗяВоЧкА:
Спасибо, это еще один способ решения, но для более старших классов. Вы можете пожалуйста объяснить чуть проще?
Попробую.
Спасибо.
Вас заинтересует
2 года назад
2 года назад
2 года назад
7 лет назад
9 лет назад