Question

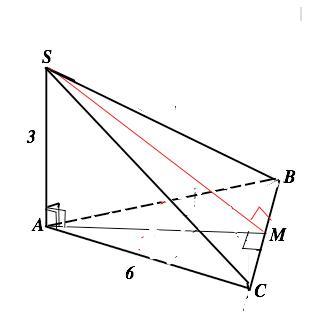
Основание треугольной пирамиды SABC - равносторонний треугольник ABC. Боковое ребро SA перпендикулярно плоскости основания. Длина стороны основания = 6 см, длина SA = 3 см. Определите площадь боковой поверхности пирамиды.

Answer 1

Ответ:36 см²

Объяснение: В пирамиде SABC боковое ребро SA перпендикулярно плоскости основания, следовательно, перпендикулярно любой прямой, лежащей в этой плоскости.=> Боковые грани SAC и ЅАВ - равные прямоугольные треугольники (по равным катетам).

Ѕ бок=Ѕ⊿ ЅАС+Ѕ⊿ ЅАВ+Ѕ ∆ ВЅС=2•Ѕ⊿ ЅАС+Ѕ ∆ ВЅС

2•Ѕ⊿ ЅАС=2•ЅА•АС:2=3•6=18 см²

Ѕ ∆СЅМ=ЅМ•СМ/2

По т.Пифагора в боковой грани  СЅМ высота  ЅМ=√(SA²+AM²)

ЅА=3 (давно)

Все углы ∆ АВС=60°

АМ=АС•sinACM=6•√3/2=3√3

ЅМ=√(9+27) =6

Ѕ ∆СЅМ=6•6/2=18 см²

Ѕ бок=18+18=36 см²