Question

найдите боковую сторону равнобедренного треугольника если угол между ними равен 120 градусам а медиана проведенная к боковой стороне равна 14 см

Answer 1

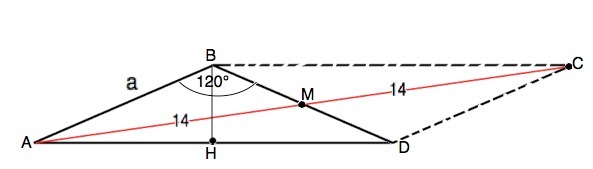
Обозначим вершины треугольника А,В,D. 

Примем АВ=ВD=а. 

Проведем высоту ВН. 

Угол АВН=120°:2=60°

 АН=а•sin60°=a√3/2

AD=2•AH=a√3

Продлим медиану АМ на ее длину до т.С. 

АМ=МС; ВМ=МD ⇒ диагонали АВСD точкой пересечения делятся помолам. ⇒АВСD - параллелограмм. 

AB=BD=CD; BC=AD

АС=28

В параллелограмме сумма квадратов диагоналей равна сумме квадратов всех его сторон. 

ВD*+AC²=AB²+CD²+BC²+AD²

а²+28²=2а²+2•3а²

7а²=28•7•4

а=√(7•4•4)=4√7 см