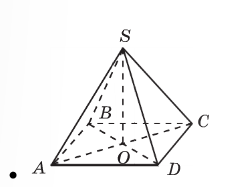
К плоскости квадрата АВСD проведено перпендикуляр OS.Докажите ,что плоскости SAC и SBD взаимно перпендикулярны.
Приложения:
Ответы
Ответ дал:
16
SO ┴ (ABCD)⇒SO ┴ AO ⇔ AO ┴ SO .
Плоскость ASC проходит через прямой AO или AO ∈ (ASC) ;причем
AO ┴ SO [ SO∈(SBD) ] и AO ┴ BD [ BD∈SBD] ⇒Плоскость треугольника SAC
проходит через прямую AO перпендикулярную к другой плоскости (плоскость SBD)
значит плоскости SAC и SBD взаимно перпендикулярны (признак перпендикулярности двух плоскостей).
Плоскость ASC проходит через прямой AO или AO ∈ (ASC) ;причем
AO ┴ SO [ SO∈(SBD) ] и AO ┴ BD [ BD∈SBD] ⇒Плоскость треугольника SAC
проходит через прямую AO перпендикулярную к другой плоскости (плоскость SBD)
значит плоскости SAC и SBD взаимно перпендикулярны (признак перпендикулярности двух плоскостей).
Вас заинтересует
2 года назад
2 года назад
2 года назад
7 лет назад
7 лет назад
9 лет назад
9 лет назад