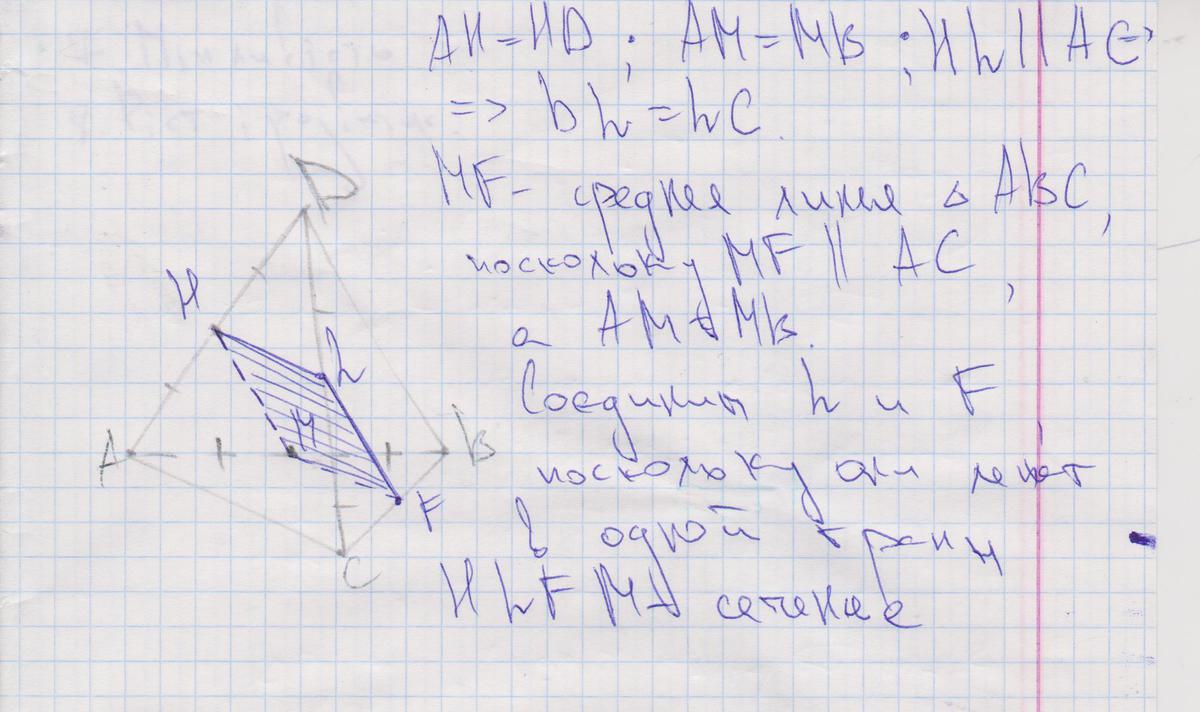
построить сечение правильного тетраэдра dabc проходящего через середины ребер ad и ab параллельно ребру ac
Ответы
Ответ дал:
8
Ответ находиться во вложении
Приложения:
Ответ дал:
2
Пусть М - середина AB, N - Середина АD, P - середина BC, Q - середина CD. Тогда PMNQ - искомое сечение. Действительно PM||AC как средняя линия треугольника ABC и QN||AC как средняя линия треугольника ACD. Значит AC параллельна двум прямым PM и QN лежащим в плоскости PMNQ, т.е. параллельна и самой плоскости. При этом стороны четырехуольника PMQN лежат на гранях тетраэдра. Значит это сечение.
Вас заинтересует
2 года назад
2 года назад
2 года назад
7 лет назад
7 лет назад