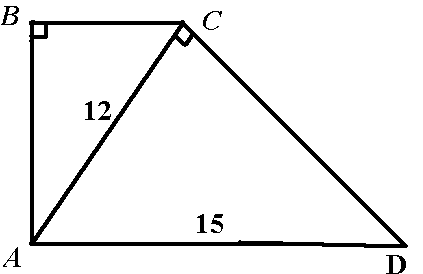
В прямоугольной трапеции ABCD (AD‖BC, AB перпендикулярна CD) большее основание AD = 15 см, диагональ АС перпендикулярна CD, AC = 12 см. Найти меньшее основание
трапеции
Приложения:
Ответы
Ответ дал:
2
ΔАСD: по теореме Пифагора AD²=AC²+CD²
15²=12²+CD², CD=9 см
CH - высота ΔACD
пусть АН= х см, тогда НD=(15-x) см
ΔAHC:
по теореме Пифагора АС²=СН²+АН², 12²=х²+СН². СН²=12²-х², СН²=144-х²
ΔCHD:
по теореме Пифагора CD²=CH²+HD², 9²=CH²+(15-x)², CH²=-144+30x-x²
CH - общая сторона для ΔAHC и ΔDHC
144-x²=-144+30x-x²
30x=288
x=9,6
AH=BC=9,6
ответ: меньшее основание трапеции =9, 6 см
15²=12²+CD², CD=9 см
CH - высота ΔACD
пусть АН= х см, тогда НD=(15-x) см
ΔAHC:
по теореме Пифагора АС²=СН²+АН², 12²=х²+СН². СН²=12²-х², СН²=144-х²
ΔCHD:
по теореме Пифагора CD²=CH²+HD², 9²=CH²+(15-x)², CH²=-144+30x-x²
CH - общая сторона для ΔAHC и ΔDHC
144-x²=-144+30x-x²
30x=288
x=9,6
AH=BC=9,6
ответ: меньшее основание трапеции =9, 6 см
Вас заинтересует
2 года назад
2 года назад
2 года назад
7 лет назад
7 лет назад
9 лет назад