Ответы
Ответ дал:
4
Раскрытие модуля в общем случае:

Приравняем подмодульное выражение к нулю и решим уравнение:
x-1=0 ⇒ x=1
Значит, нужно раскрыть модуль в двух случаях: x>1 и x<1 (х=1 не рассматриваем, так как в этом случае знаменатель дроби равен 0, чего не может быть):

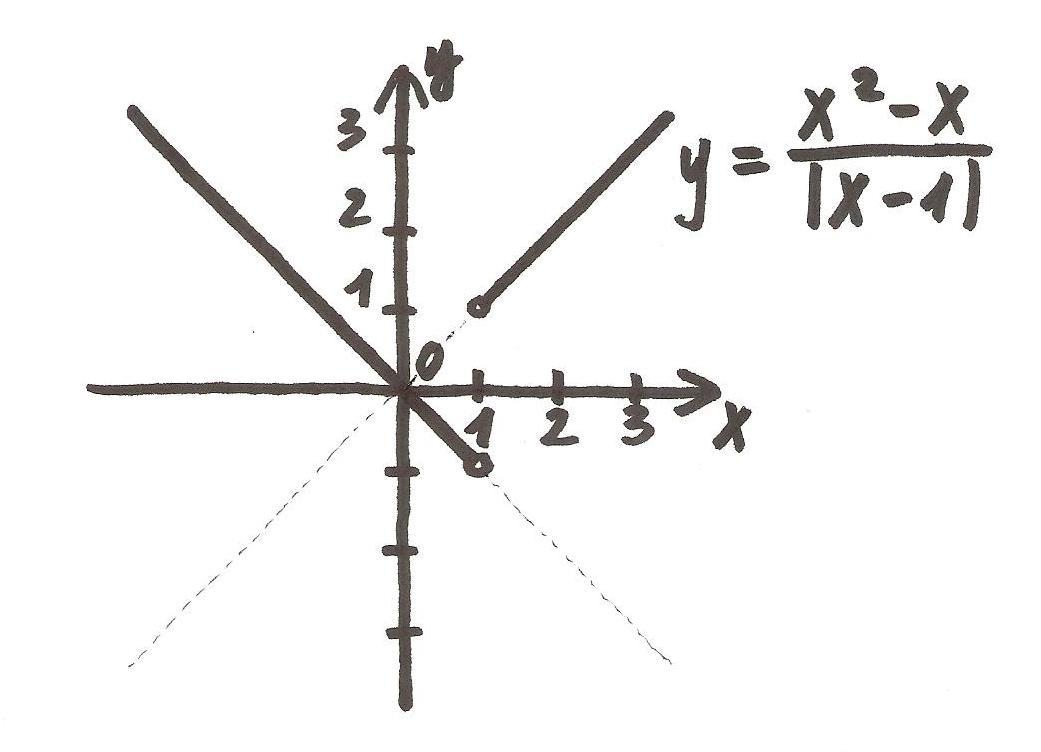
Строим прямую у=х (биссектриса первого и третьего координатного угла) на интервале х>1 и прямую у=-х (биссектриса второго и четвертого координатного угла) на интервале х<1, учитывая точку разрыва х=1, в которой функция не определена (картинка)
Приравняем подмодульное выражение к нулю и решим уравнение:
x-1=0 ⇒ x=1
Значит, нужно раскрыть модуль в двух случаях: x>1 и x<1 (х=1 не рассматриваем, так как в этом случае знаменатель дроби равен 0, чего не может быть):
Строим прямую у=х (биссектриса первого и третьего координатного угла) на интервале х>1 и прямую у=-х (биссектриса второго и четвертого координатного угла) на интервале х<1, учитывая точку разрыва х=1, в которой функция не определена (картинка)
Приложения:
GreatFilter:
Спасибо
Вас заинтересует
2 года назад
2 года назад
2 года назад
7 лет назад
7 лет назад
9 лет назад