Question

докажите что поворот плоскости вокруг точки является движением. ПОМОГИТЕ ПОЖАЛУЙСТА!!

Answer 1

Движение – отображение плоскости на себя, при котором расстояния между точками плоскости сохраняются.

Докажем, что поворот является движением, то есть, при повороте сохраняются расстояния между точками.

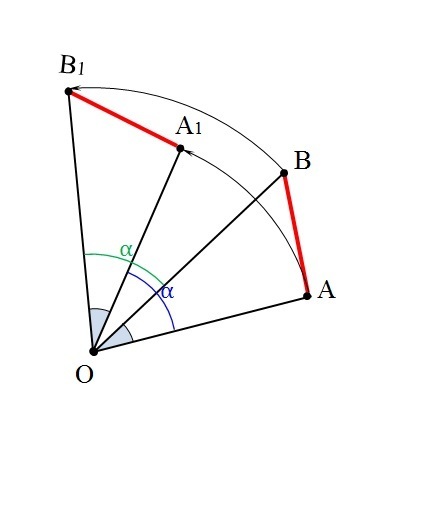
Возьмём две произвольные точки на плоскости: А и В. Выберем точку О – центр поворота и угол поворота α. При этом повороте точка А переходит в точку А1, точка В в точку В1.

По определению поворота: ОА = ОА1; ОВ = ОВ1; ∠АОА1 = α; ∠ ВОВ1 = α

Рассмотрим ∆АОВ и ∆А1ОВ1.

∠АОВ = α  – ∠ВОА1; ∠А1ОВ1 = α – ∠ВОА1 ⇒ ∠АОВ = ∠А1ОВ1

и  ОА = ОА1; ОВ = ОВ1.

Следовательно, треугольники равны по двум сторонам и углу между ними.

Раз треугольники равны, то равны соответственные стороны, 

тогда АВ = А1В1.

Это и говорит о том, что расстояние между двумя точками при повороте осталось без изменения. Точки А и В выбраны произвольным образом, поэтому можно сделать вывод, что сохранятся расстояния между любыми двумя точками.
Чертёж на приложенном изображении.