Ответы
Ответ дал:
0
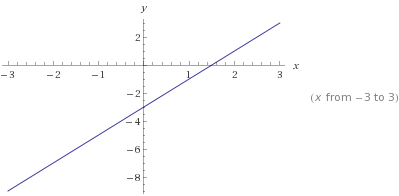
Знаменатель не может равняться 1, следовательно, х не равно 1. В этом случае формула функции упрощается до

Это линейная функция, строится по двум точкам. График приложен.
Это линейная функция, строится по двум точкам. График приложен.
Приложения:
ZayacZnaniy:
то есть мы имеем у=2-3х и просто строим график без каких либо ограничений?
С ограничением: х не может равняться 1. То есть х=1 - выколотая точка
Ответ дал:
1
область определения
х ≠ 1
график смотри в приложенном файле
это прямая (.т.к. числитель и знаменатель можно сократить на (х-1) при х ≠1)
прямая разорвана в точке х = 1
х ≠ 1
график смотри в приложенном файле
это прямая (.т.к. числитель и знаменатель можно сократить на (х-1) при х ≠1)
прямая разорвана в точке х = 1
Приложения:
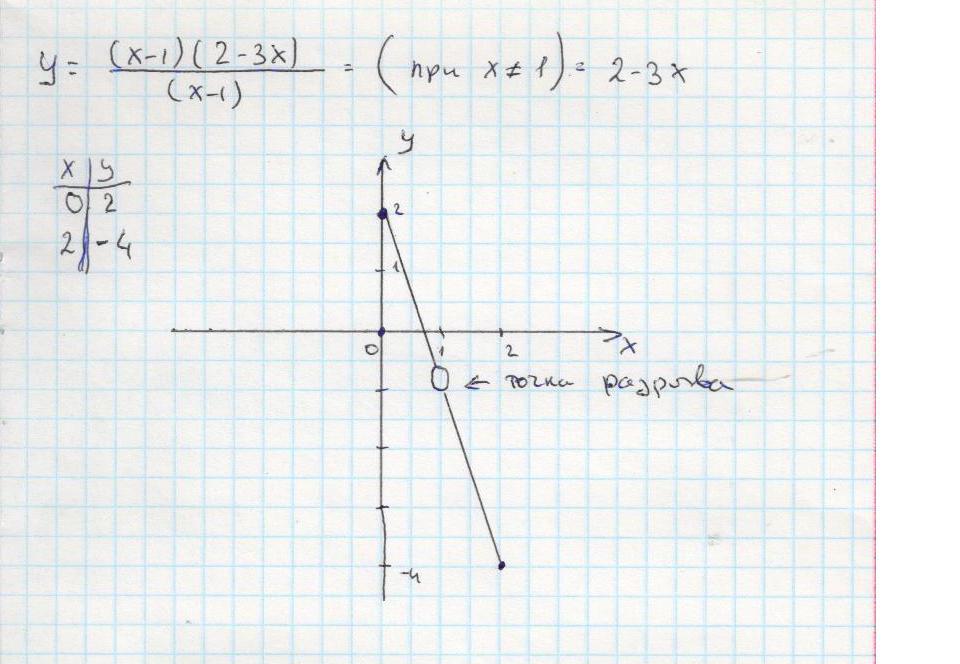
вот теперь все) спасибо!!))
попробуйте еще раз, excel действительно криво пошел, а эта картинка - норм.
слава богу)))
то есть там где точка разрыва просто пустое место?
там обычно ставят такой круглешок, чтобы обозначить, что это не просто лениво рисовать было, а именно точка разрыва.
спасибо, но мы это не проходили ..
точнее нам никто никогда об этом не говорил..
бывает))) От нас тоже многое скрывают
большое спасибо за помощь!
рад помочь)
Вас заинтересует
2 года назад
2 года назад
7 лет назад
7 лет назад
9 лет назад