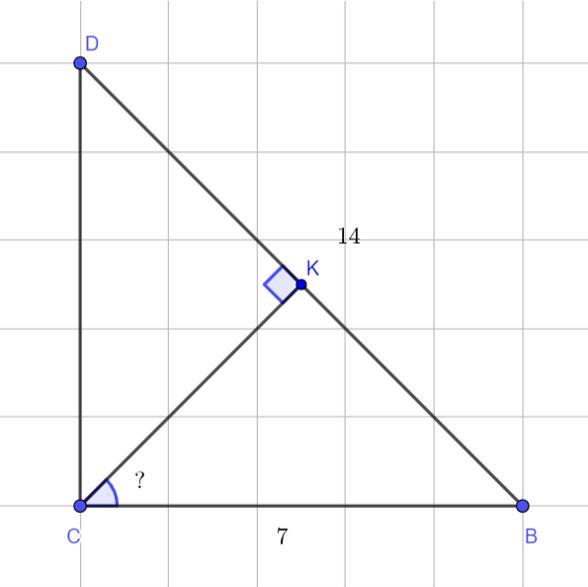
В прямоугольном треугольнике DBC ( угол C - 90 градусов ) провели высоту СК . Найдите угол ВСК , если DВ- 14 см , ВС-7 см .
Ответы
Ответ дал:
8
DВ является гипотенузой треугольника DBC, а ВС — катетом.
DВ = ВС ∙ 2.
В прямоугольном треугольнике катет, равный половине гипотенузы, лежит против угла 30°.
Это значит, что ∠CDB = 30°.
Сумма острых углов прямоугольного треугольника равна 90°, поэтому ∠KBC = 90 - 30 = 60°.
Рассмотрим треугольник KBC.
∠CKB = 90°, потому что CK — высота, а это означает, что CK ⊥ DB.
∠KBC + ∠ВСК = 90°.
Отсюда, ∠ВСК = 90 - 60 = 30°.
Ответ: 30°.
Приложения:
Вас заинтересует
2 года назад
2 года назад
2 года назад
2 года назад
7 лет назад
7 лет назад
9 лет назад