Question

В шар радиус р вписан конус...... Найти площадь...... если угол а 30. Найти наибольшую площадь сечения проходящую через вершину конуса

Answer 1

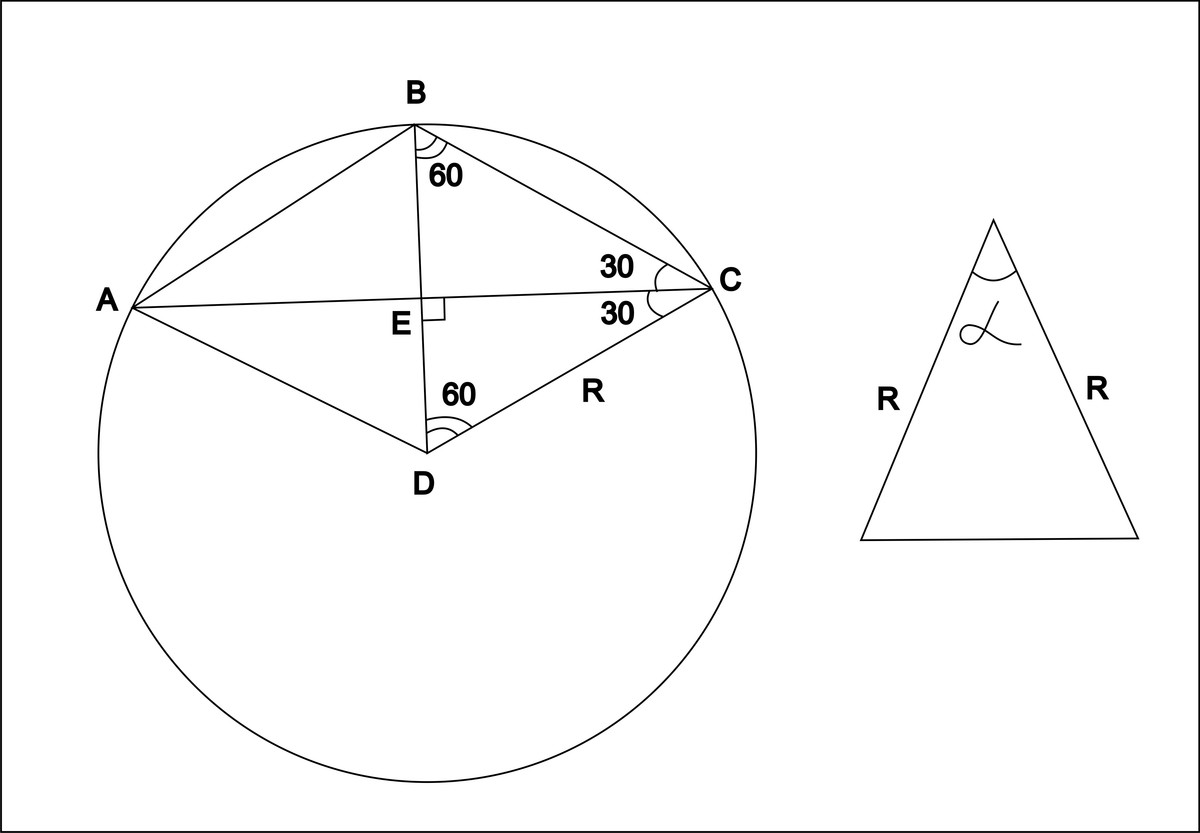
D-центр окружности
поскольку BD=DC=R то угол DBC=BCD=60
угол BDC=180-60-60=60
получается треугольник BDC равносторонний
ВЕ=ВСsin30=R/2
EC²=BC²-EB²=R²-(R²/4)=(3R²)/4
S(боковой поверхности)=πrl=π·EC·BC=(π√3R²)/2

сечение проходящее через вершину треугольника будет равнобедренным треугольником с боковыми сторонами=R 
площадь треугольника равна произведению сторон прилегающих к углу на синус угла между ними
S=(1/2)·R²·sinα
α ∈ (0;120]
sin принимает наибольшее значение при α=90
sin90=1
S=(1/2)·R²·sin90=R²/2