высота правильной четырехугольной пирамиды равна 4 м, а диагональ основания - 10 м. найти площадь ее боковой поверхности.
Ответы
Ответ дал:
1
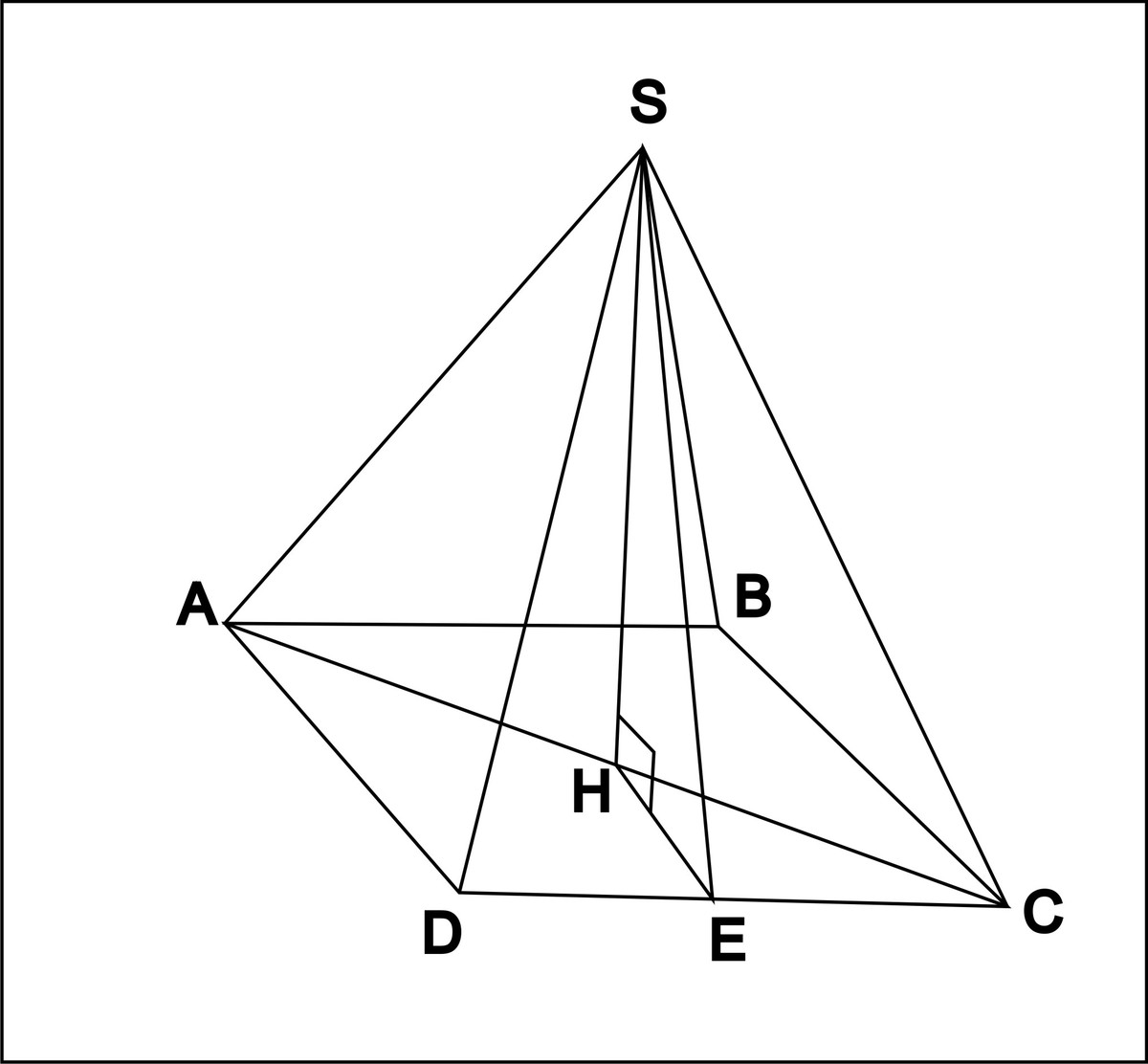
DC²+BC²=DB²
DC=BC
2DC²=100
DC=5√2
HD=(1/2)DB=5
в треугольнике SHD
SD²=SH²+HD²
SD=√41
DE=(1/2)DC=(5√2)/2
в треугольнике SDE
SE²=SD²-DE²
SE=(√114)/2
S(боковой поверхности)=4S(SDC)=4·SE·DC·(1/2)=10√57
DC=BC
2DC²=100
DC=5√2
HD=(1/2)DB=5
в треугольнике SHD
SD²=SH²+HD²
SD=√41
DE=(1/2)DC=(5√2)/2
в треугольнике SDE
SE²=SD²-DE²
SE=(√114)/2
S(боковой поверхности)=4S(SDC)=4·SE·DC·(1/2)=10√57
Приложения:
Вас заинтересует
2 года назад
2 года назад
2 года назад
2 года назад
7 лет назад
7 лет назад
9 лет назад