ДАЮ 100 БАЛЛОВ!!! нужно решить этот предел правилом лопиталя.
ответ известен, но какие шаги???
Приложения:
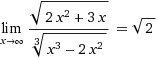
Ответы
Ответ дал:
1
Anton1702:
ответы расходятся??????
АУ! перепроверьте, пожалуйста!
вы вроде забыли вынести степень перед множителем по правилу производной
Вас заинтересует
2 года назад
2 года назад
2 года назад
2 года назад
7 лет назад
7 лет назад
9 лет назад