Ответы
Ответ дал:
1
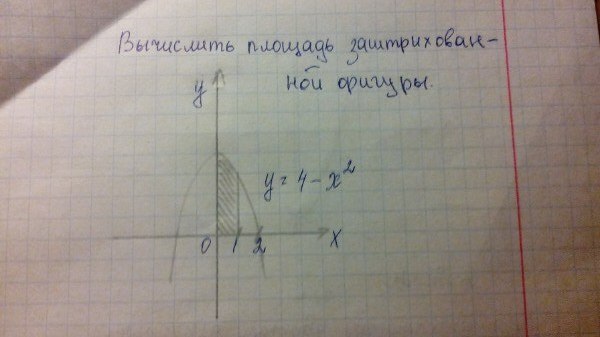
Первообразная подынтегральной функции будет равна:
Далее находим площадь как разность F(1) - F(0)
(4·1-1³/3+C)-(4*0-0³/3+C)=4-1/3= 3 и 2/3
Ответ: Площадь заштрихованной фигуры равна
Ответ дал:
1
С чертежа списываем пределы интегрирования,затем находим первообразную и подставляем значения Х.
Приложения:
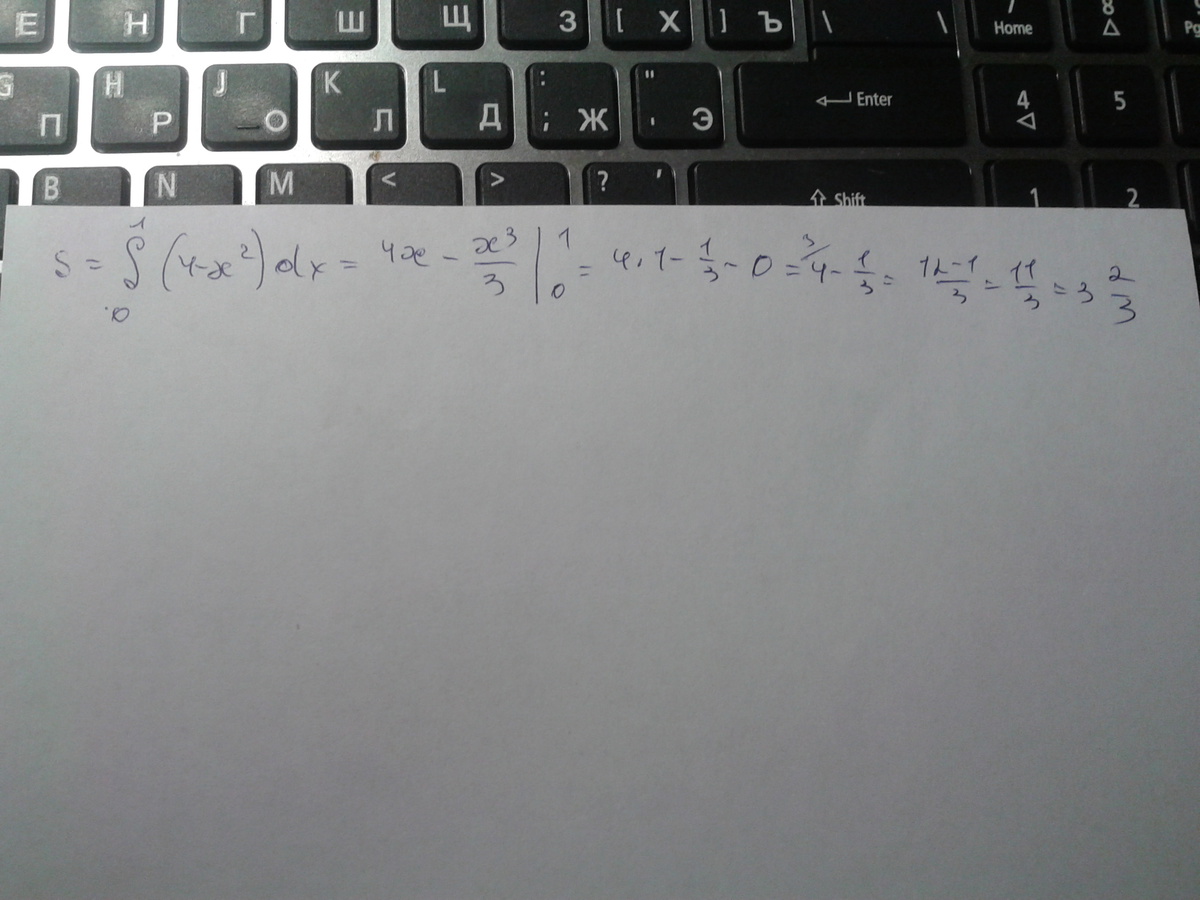
Вас заинтересует
2 года назад
2 года назад
2 года назад
7 лет назад
7 лет назад
9 лет назад