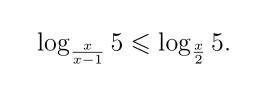Ответы
Ответ дал:
1
Для начала записываем ОДЗ





Дальше перевернем логарифмы, перейдем к основанию 5.


Основание логарифма 5>1, значит при переходе к алгебраическому неравенству менять знак неравенства не надо.




На числовую ось наносим все нули дробно рационального уравнения и ОДЗ. то есть x=0, x=3 и
Расставляем знаки в интервалах. получаем ответ (-∞,0] U (1, 3]
теперь проверим, все ли из ответа входит в ОДЗ.
Точка x=2 выкидываем из ответа, и промежуток (-∞,0].
В ответ пойдет (1,2)U(2,3]
Дальше перевернем логарифмы, перейдем к основанию 5.
Основание логарифма 5>1, значит при переходе к алгебраическому неравенству менять знак неравенства не надо.
На числовую ось наносим все нули дробно рационального уравнения и ОДЗ. то есть x=0, x=3 и
Расставляем знаки в интервалах. получаем ответ (-∞,0] U (1, 3]
теперь проверим, все ли из ответа входит в ОДЗ.
Точка x=2 выкидываем из ответа, и промежуток (-∞,0].
В ответ пойдет (1,2)U(2,3]
olenka90:
сделала промежуток, а дальше как?
Вас заинтересует
2 года назад
2 года назад
2 года назад
7 лет назад
9 лет назад