Ответы
Ответ дал:
0
..........................................................
Приложения:
Ответ дал:
1
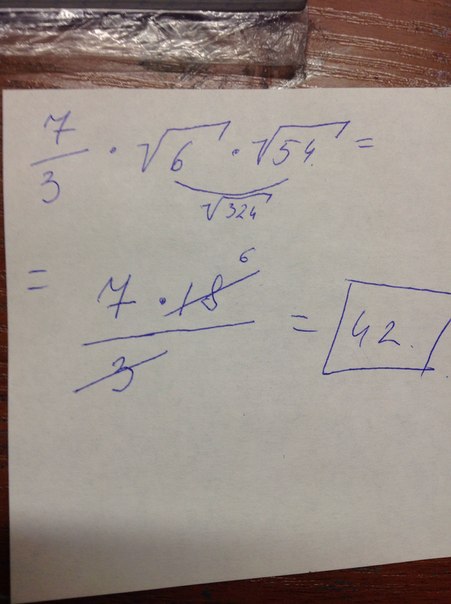
Произведение квадратных корней двух чисел равно квадратному корню из произведения этих чисел:

Далее представим 54 в виде произведения чисел 6 и 9 и увидим, что под корнем у нас квадрат числа:

Квадратный корень из квадрата числа равен этому числу:

Чтобы умножить дробь на число, умножаем числитель дроби на это число:

Полная запись решения будет выглядеть так:

Далее представим 54 в виде произведения чисел 6 и 9 и увидим, что под корнем у нас квадрат числа:
Квадратный корень из квадрата числа равен этому числу:
Чтобы умножить дробь на число, умножаем числитель дроби на это число:
Полная запись решения будет выглядеть так:
Вас заинтересует
2 года назад
2 года назад
2 года назад
2 года назад
7 лет назад