Question

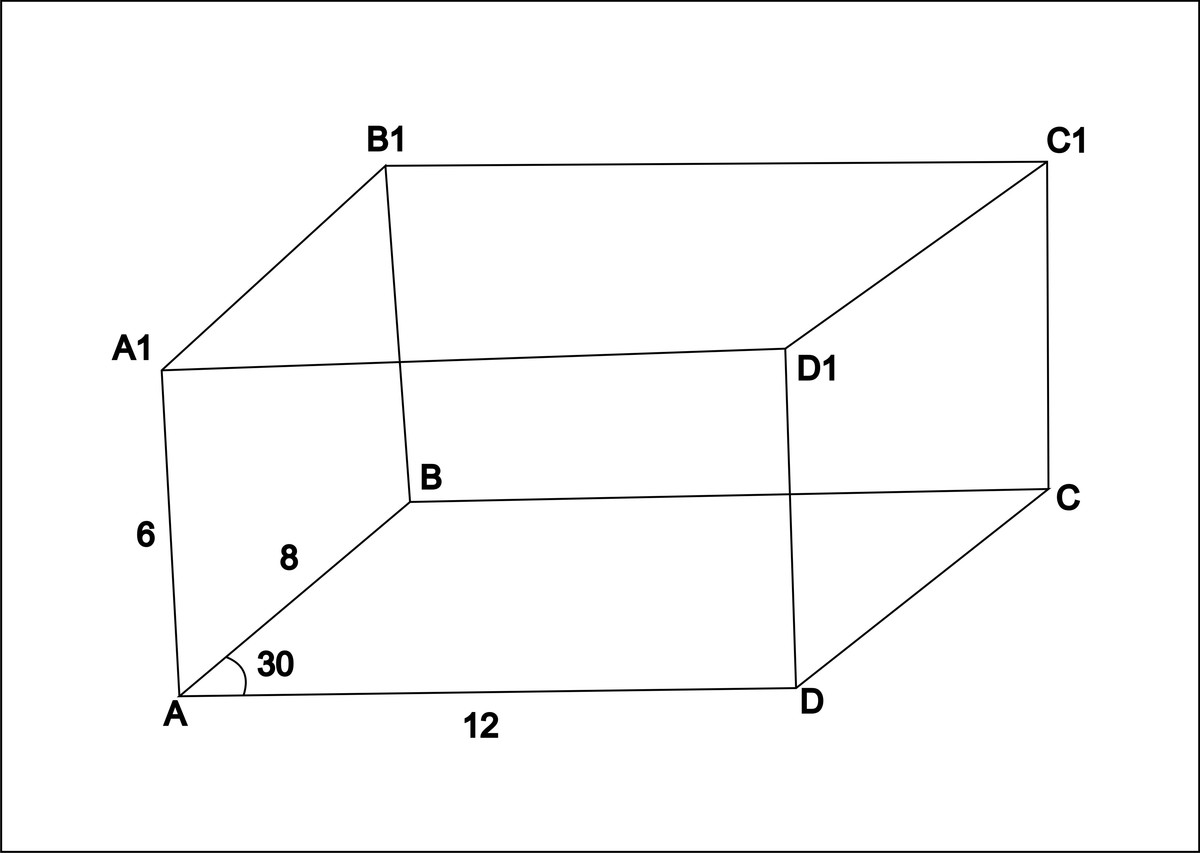
найдите полную поверхность прямого параллелепипед, стороны основания которого равны 8 дм и 12 дм и образуют угол в 30, а боковое ребро равно 6 дм

Answer 1

площадь параллелограмма равна синусу угла на произведение прилегающих сторон
S(ABCD)=AB·AD·sinA=8·12·sin30=48
S(боковой поверхности)=2S(AA1D1D)+2S(BB1A1A)=6·12·2+6·8·2=240
S(всей поверхности)=2S(ABCD)+S(боковой поверхности)=336