КАК РЕШАТЬ? ПОМОГИТЕ!!! ТОЛЬКО С ОБЪЯСНЕНИЯМИ!!!
Приложения:
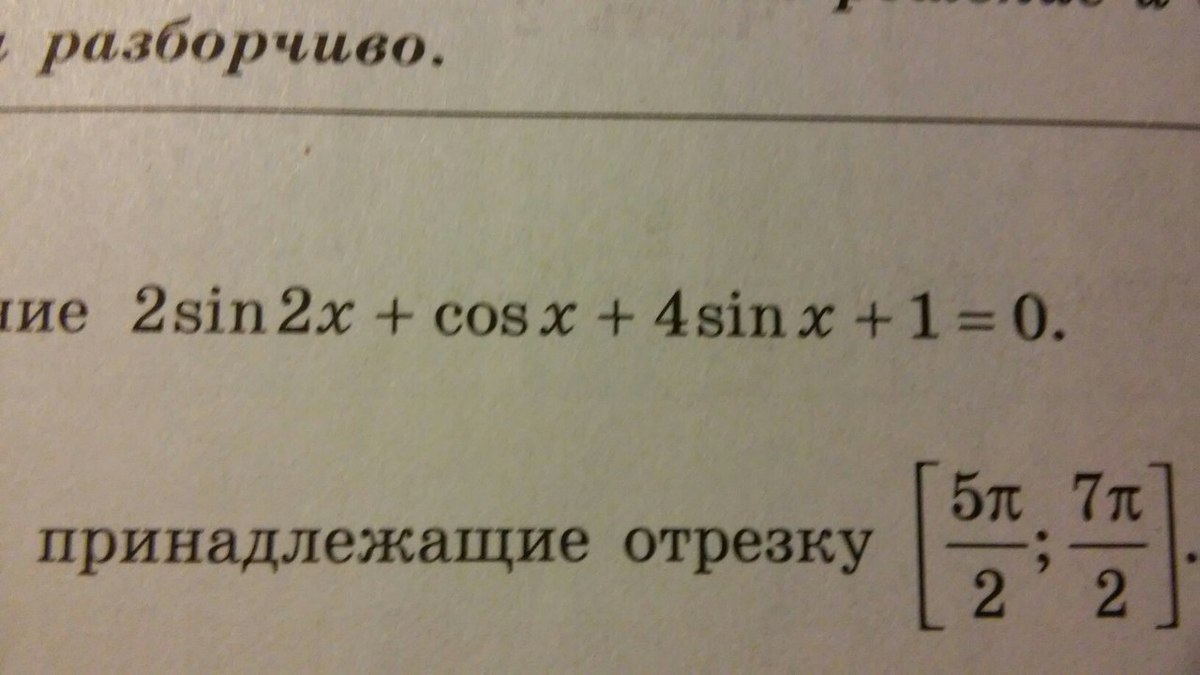
Елизавета8953:
ПОМОГИ ПЛИИИЗ
1 НОМЕР
Ответы
Ответ дал:
0
2sin2x +cosx+4sinx+1=0
2(2sinx cosx) + cosx + 4sinx+1=0
(4sinx cosx+cosx) + (4sinx +1)=0
cosx(4sinx+1) + (4sinx+1)=0
(4sinx+1)(cosx+1)=0
4sinx+1=0 cosx+1=0
4sinx=-1 cosx=-1
sinx=-1/4 x=π+2πn, n∈Z
x=(-1)^(n+1) arcsin 1/4 +πn, n∈Z
На промежутке [5π; 7π]
2 2
по синусоиде y=sinx:
n=3 x=(-1)³⁺¹ arcsin 1/4 +3π
x=arcsin 1/4 +3π
по косинусоиде у=cosx:
n=1 x=π+2π
x=3π
Ответ: arcsin 1/4+3π; 3π.
2(2sinx cosx) + cosx + 4sinx+1=0
(4sinx cosx+cosx) + (4sinx +1)=0
cosx(4sinx+1) + (4sinx+1)=0
(4sinx+1)(cosx+1)=0
4sinx+1=0 cosx+1=0
4sinx=-1 cosx=-1
sinx=-1/4 x=π+2πn, n∈Z
x=(-1)^(n+1) arcsin 1/4 +πn, n∈Z
На промежутке [5π; 7π]
2 2
по синусоиде y=sinx:
n=3 x=(-1)³⁺¹ arcsin 1/4 +3π
x=arcsin 1/4 +3π
по косинусоиде у=cosx:
n=1 x=π+2π
x=3π
Ответ: arcsin 1/4+3π; 3π.
Ответ дал:
0
2sin2x+cosx+4sinx+1=0
2*2sinxcosx+cosx+4sinx+1=0
(2*2sinxcosx+cosx)+4sinx+1=0
cosx(4sinx+1)+(4sinx+1)=0
(cosx+1)(4sinx+1)=0
cosx+1=0 4sinx+1=0
cosx=-1 4sinx=-1
x=pi+2pin, n∈z sinx=-1/4
x=(-1)k+1arcsin 0,25+ pik,k∈z
теперь найдем корни для нашего промежутка:
1) 5pi/2 =<pi+2pin=<7pi/2 (1/pi)
5/2=<1+2n=<7/2 (2)
5=<2+4n=<7
3=<4n=<5
3/4=<n=<5/4
n=1
x=pi+2pi= 3pi
x=3pi
2) теперь найдем для второго уравнения:
3pi+arcsin(1/4)
все это находится по тригонометрической окружности
2*2sinxcosx+cosx+4sinx+1=0
(2*2sinxcosx+cosx)+4sinx+1=0
cosx(4sinx+1)+(4sinx+1)=0
(cosx+1)(4sinx+1)=0
cosx+1=0 4sinx+1=0
cosx=-1 4sinx=-1
x=pi+2pin, n∈z sinx=-1/4
x=(-1)k+1arcsin 0,25+ pik,k∈z
теперь найдем корни для нашего промежутка:
1) 5pi/2 =<pi+2pin=<7pi/2 (1/pi)
5/2=<1+2n=<7/2 (2)
5=<2+4n=<7
3=<4n=<5
3/4=<n=<5/4
n=1
x=pi+2pi= 3pi
x=3pi
2) теперь найдем для второго уравнения:
3pi+arcsin(1/4)
все это находится по тригонометрической окружности
Вас заинтересует
2 года назад
2 года назад
7 лет назад
7 лет назад
9 лет назад