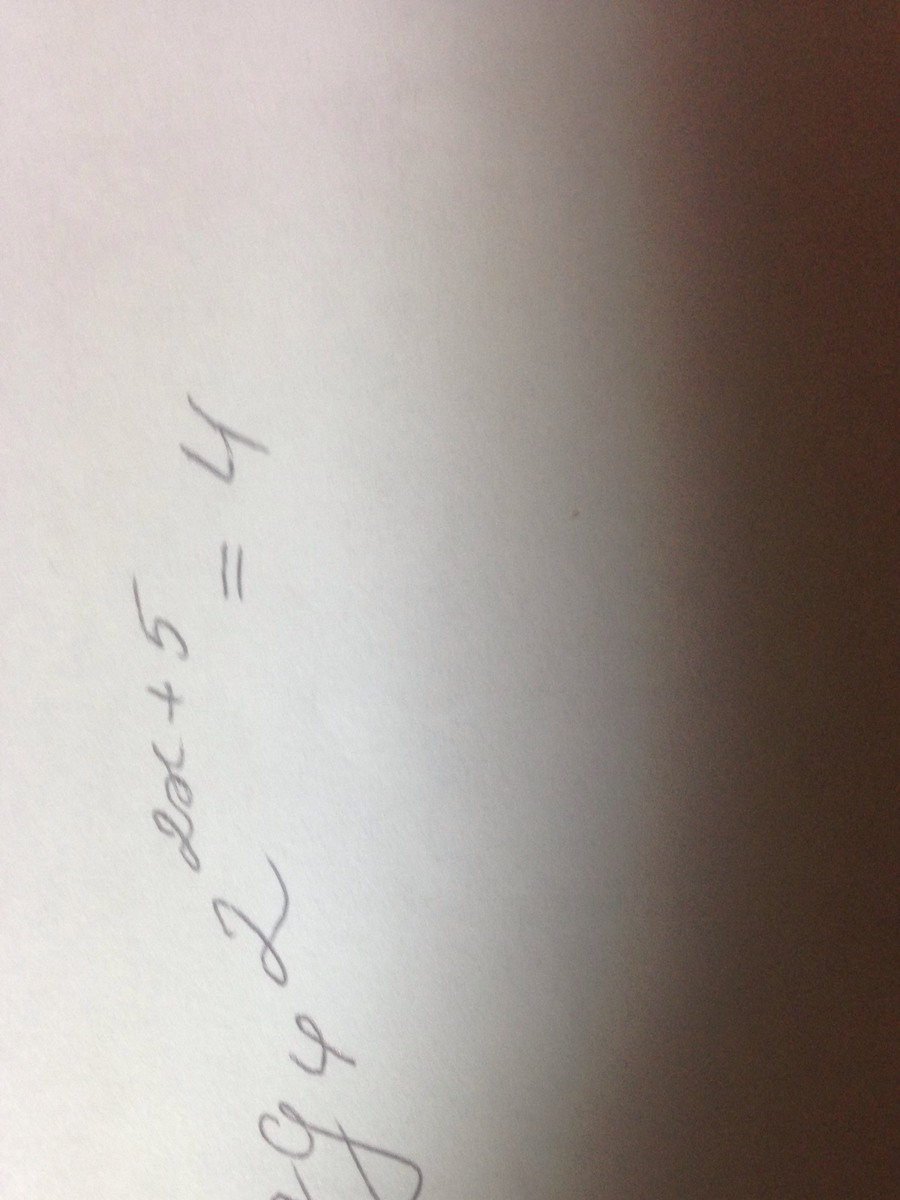Ответы
Ответ дал:
1
Аноним:
Там логарифм есть))
у меня вопрос, а откуда 256?
log4 (4^4)
4^4=256
спасибо!
Ответ дал:
1
log4 (2^(2x+5))=4
log4 (2^(2x+5))=4log4 4
2^(2x+5)=(2²)^4
2x+5=8
2x=8-5
2x=3
x=1.5
log4 (2^(2x+5))=4log4 4
2^(2x+5)=(2²)^4
2x+5=8
2x=8-5
2x=3
x=1.5
Вас заинтересует
2 года назад
2 года назад
2 года назад
2 года назад
7 лет назад
7 лет назад
9 лет назад
9 лет назад