Помогите пожалуйста разобраться, какие нужно провести преобразования с первым выражением, что бы получить именно второе выражение?
Приложения:
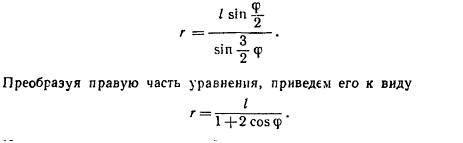
Ответы
Ответ дал:
0
sin(3x/2)=sin(x/2+x)=sin(x/2)cos(x)+cos(x/2)sin(x)=
=sin(x/2)cos(x)+2cos²(x/2)sin(x/2)=sin(x/2)(cos(x)+1+cos(x))=sin(x/2)(1+2cos(x)).
Значит l*sin(x/2)/sin(3x/2)=l/(1+2cos(x/2)).
=sin(x/2)cos(x)+2cos²(x/2)sin(x/2)=sin(x/2)(cos(x)+1+cos(x))=sin(x/2)(1+2cos(x)).
Значит l*sin(x/2)/sin(3x/2)=l/(1+2cos(x/2)).
Вас заинтересует
2 года назад
2 года назад
2 года назад
2 года назад
7 лет назад
7 лет назад
9 лет назад