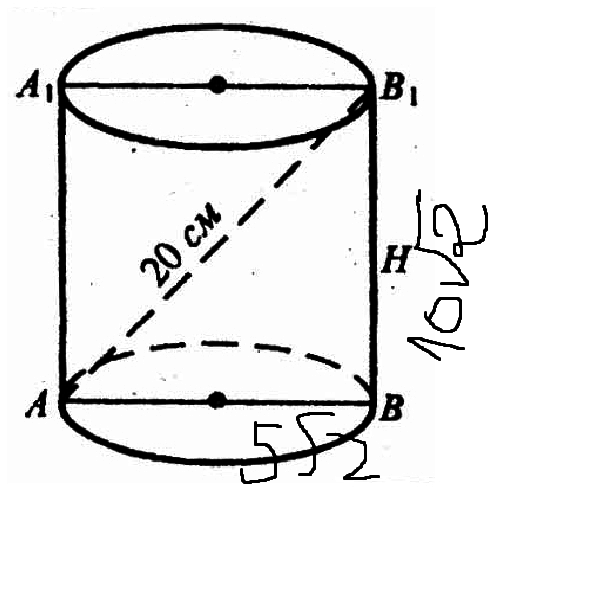
Осевое сечение цилиндра-квадрат,диагональ которого равна 20 см. Найди площадь основания цилиндра.
Ответы
Ответ дал:
10
Так как осевым сечением является квадрат то его диагональ равна:  ,где
,где  - сторона квадрата,тогда:
- сторона квадрата,тогда:
 (см)
(см)
Δ -прямоугольный,тогда:
-прямоугольный,тогда:

S основания =
 (см)
(см)
 (см)
(см)
Ответ: (см)
(см)
Δ
S основания =
Ответ:
Приложения:
Вас заинтересует
2 года назад
2 года назад
2 года назад
2 года назад
7 лет назад
9 лет назад