Question

Биссектрисы углов трапеции,прилежащих к боковой стороне CD,пересекаются в точке О.Найдите расстояние от точки О до середины отрезка CD,если CD=12см.Решение распишите подробно с рисунком.Заранее большое спасибо;)Удачи вам!

Answer 1

Рисунок в файле.
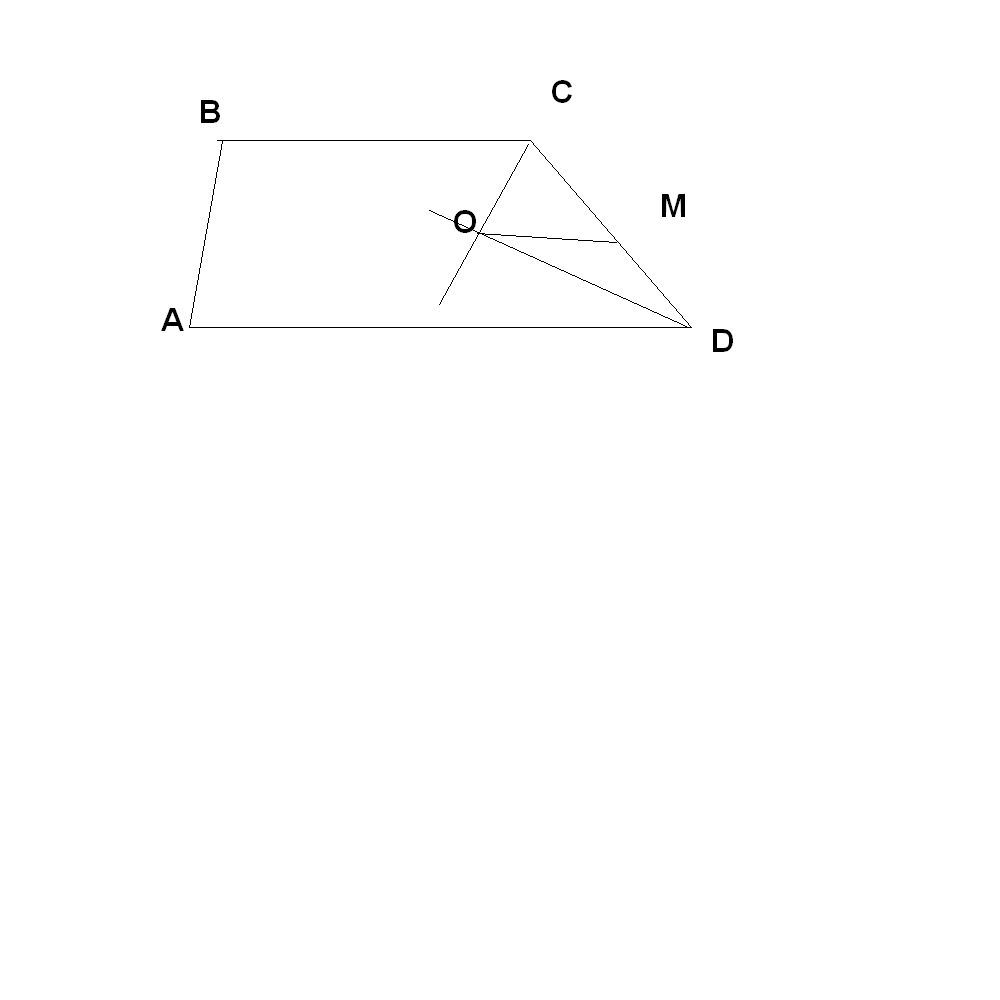
т.к. у трапеции сумма углов при боковой стороне = 180, тогда ОСД+СДО=(С+Д)/2=180/2=90  (СО и ДО - биссектрисы,)
соответственно угол СОД=90 
треуг. СОД прямоугольный, СД - гипотенуза.
Если вокруг него описать окружность, то центр как раз будет в т.М (на середине гипотенузы), и тогда  радиус ее R=OM=CM=DM=CD/2=12/2=6