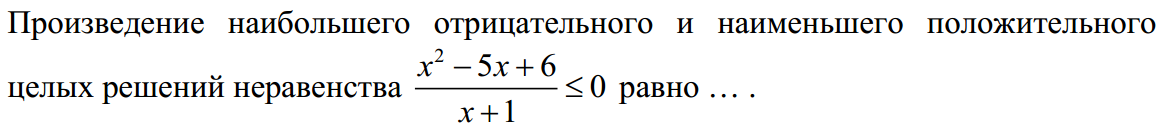Ответы
Ответ дал:
2
Подобные неравенства решаются методом интервалов. В этом методе мы находим все точки, в которых выражение(в данном случае и числитель и знаменатель) обращаются в 0. Потом эти точки отмечаем на прямой, и находим знаки интервалов. А от туда записываем ответ.
Итак, к делу:
Числитель:
В итоге, наше неравенство выглядит таким образом:
Теперь рисуем прямую, отмечаем точки и находим знаки промежутков. (см. рисунок)
Обратите внимание, что точка -1 "выколота", так при 1, в знаменателе получается 0, а на 0 делить нельзя.
В ответ записываем промежутки, в которых стоит знак -
Произведение наибольшего отрицательного целого корня (-2) и наименьшего целого корня(2):
Ответ: -4.
Приложения:
Denik777:
вообще-то в задаче спрашивалось не это...
Да. Забыл о главном.
Решение изменено.
В принципе можно было не решать, а подставить точки -1,1,-2,2 и убедиться - что -2 наибольшее отрицательное, а 2 - наименьшее положительное :)
Многие примеры решаются в уме. Например предел при х стремящимся к бесконечности (3x^5+x^4-2x^3+x^2-x+7)/(x^5-3x^4+x^3-2x^2+2x-3) (Ответ: 3)
Но, важно решение.
Но, важно решение.
это было бы вполне обоснованным решением. И более коротким. Но, такое решение можно найти только когда знаешь ответ :)
Если я не ошибаюсь вы еще можете добавить свой ответ.
да ладно, я и так уже все высказал, что хотел :)
Вас заинтересует
2 года назад
2 года назад
2 года назад
2 года назад
7 лет назад
7 лет назад
9 лет назад