Дана четырехугольная пирамида с прямоугольником в основании, боковые ребра которой наклонены к основанию под углом 30 градусов. Высота пирамиды 6 , если градусная мера между диагоналями прямоугольника 30 градусов. Найти объем пирамиды.
, если градусная мера между диагоналями прямоугольника 30 градусов. Найти объем пирамиды.
Ответы
Ответ дал:
1
Рассмотри треугольник AOS (см. приложение). Он прямоугольный. Так как угол SAO = 30°, то SO = 0,5AS => AS = 12√5. Найдем катет AO =  , тогда вся диагональ АС = 12√15.
, тогда вся диагональ АС = 12√15.
Так как угол между диагоналями равен 30°, то площадь прямоугольника равна: . Значит, объем пирамиды равен:
. Значит, объем пирамиды равен: 
Ответ: 1080√5
Так как угол между диагоналями равен 30°, то площадь прямоугольника равна:
Ответ: 1080√5
Приложения:
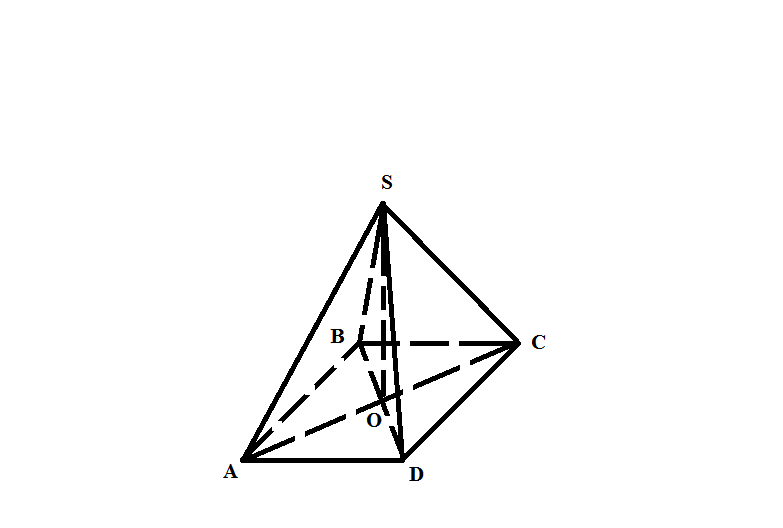
Ответ дал:
0
Смотреть во вложении
Приложения:

Вас заинтересует
2 года назад
2 года назад
2 года назад
7 лет назад
7 лет назад
9 лет назад