Ответы
Ответ дал:
7
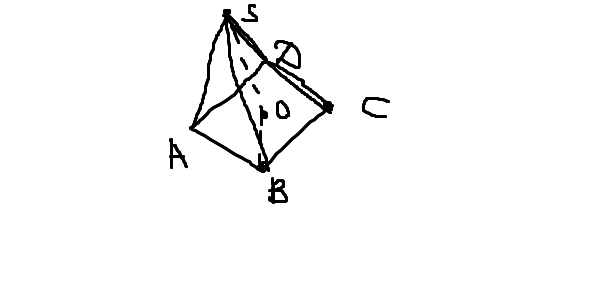
По теореме пифагора находим половину диагонали.
ОВ =

Это половина диагонали ромба(правильный четырехугольник, основание).
Диагональ ромба равна .
.
Площадь ромба равна =
= 
Объем пирамиды равен
ОВ =
Это половина диагонали ромба(правильный четырехугольник, основание).
Диагональ ромба равна
Площадь ромба равна
Объем пирамиды равен
Приложения:
Вас заинтересует
2 года назад
2 года назад
2 года назад
7 лет назад
7 лет назад
9 лет назад