Question

Вычислить площадь фигуры расположенной в первой координатной четверти и ограниченной линиями:
y=24*$\sqrt[3]{x}$ ; y=8x

Answer 1

Значит найдем точки пересечения графиков в 1-й четверти
$8x=24 \sqrt[3]{x}$
$x=3\sqrt[3]{x}$

$x^{3} =27x$
$x^3-27x=0$
$x(x^2-27)=x(x- \sqrt{27} )(x+ \sqrt{27} )=0$
отсюда точки пересечения х=0, $x= \sqrt{27}$, $x=- \sqrt{27}$
Нас интересуют только первые два корня.
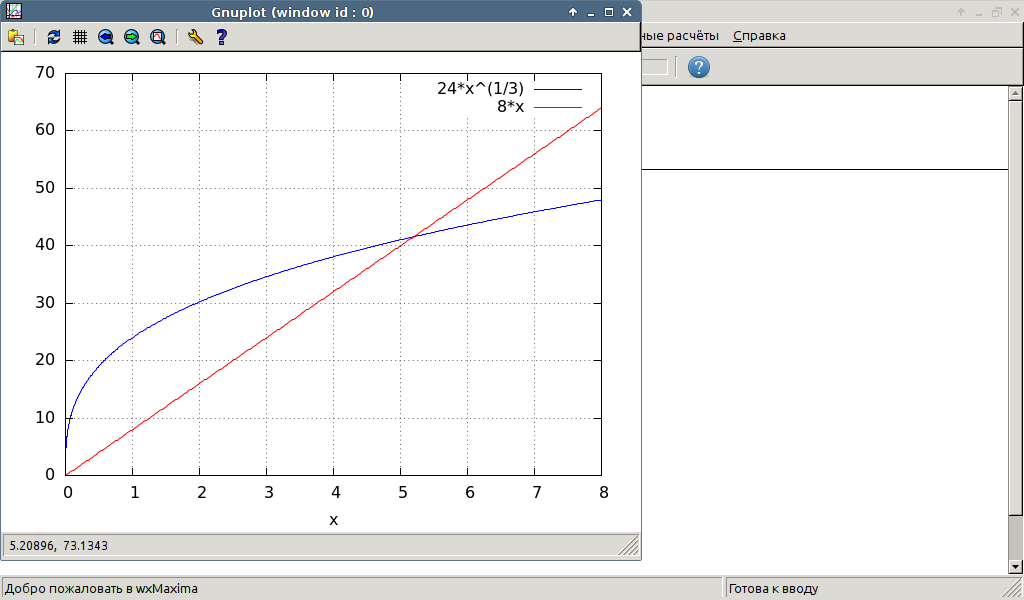
Строим рисунок, см вложение. Из рисунка видно, что полощадь искомой фигуры равна разности площадей. Площадь криволинейной трапеции - площадь треугольника. В формулах так:

$S=S_{1}-S_2= \int\limits^{x1}_0 {24 \sqrt[3]{x} } \, dx - \int\limits^{x1}_0 {8x } \, dx$  (1)
где $x1= \sqrt{27}$

Считаем интегралы в (1)
$\int\limits^{x1}_0 {24 \sqrt[3]{x} } \, dx =$
$\int\limits^{x_1}_0 {24 \sqrt[3]{x} } \, dx = 24 \int\limits^{x_1}_0 { x^{1/3} } \, dx =24*( \frac{x^{4/3}}{4/3} ) |_0^{x_1}= 24*(3 \frac{x^{4/3}}{4} ) |_0^{x_1}=$
$= 6*3x^{4/3} |_0^{x_1}= 18*x_1^{4/3}=18*27^{2/3}=3^{3*2/3}=18*3^2=18*9=162$ (2)

$\int\limits^{x1}_0 {8x } \, dx=8 \int\limits^{x1}_0 {x } \, dx= \frac{8x^2}{2} |_0^{x1}=4x_1^2= 4*27=108$  (3)
 на основании  (2) и (3) получаем
S=162-108=54
 Ответ S=54