Ответы
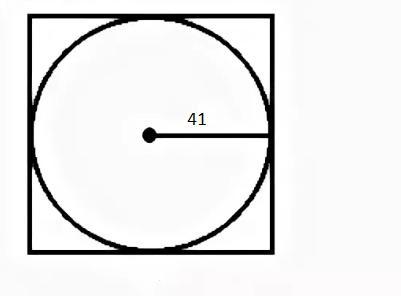
Найдите площадь квадрата, если радиус вписанной в него окружность равен 41:
Площадь квадрата определяем по формуле:
S = a², где а - сторона квадрата.
Диаметр вписанной в квадрат окружности равен ее стороне. А радиус умноженный на 2 равен диаметру. Имеем:
d = 41 * 2 = 82 (ед.)
S = 82² = 6724 (ед²)
Ответ: 6724 (ед²)
Рисунок в приложении:
Ответ:
6724
Объяснение:
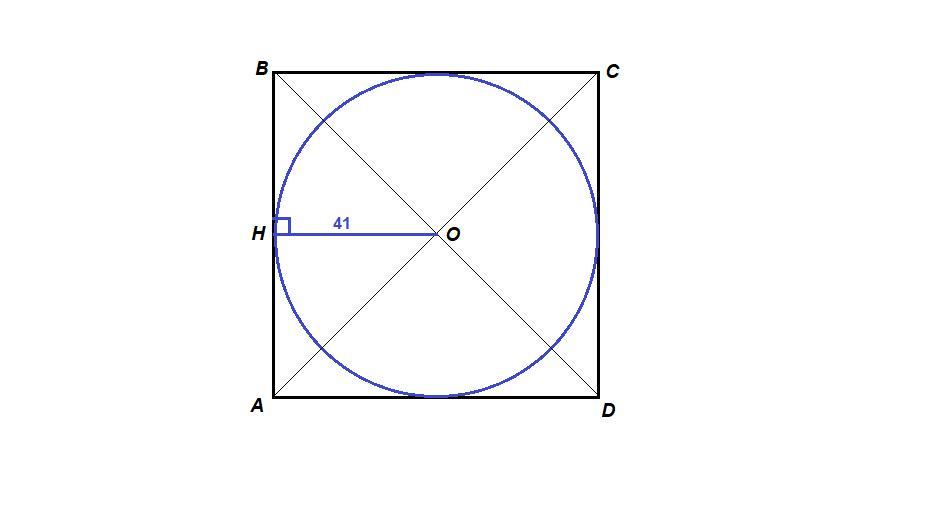
Центр окружности, вписанной в квадрат, лежит в точке пересечения его диагоналей. Диагонали точкой пересечения делятся пополам.
Проведем ОН - радиус окружности - в точку касания.
ОН⊥АВ по свойству касательной, значит ОН║AD как перпендикуляры к одной прямой.
О середина ВD, ОН║AD, значит, по теореме Фалеса, Н - середина АВ. тогда ОН - средняя линия треугольника ABD.
AD = 2OH = 2 · 41 = 82
Sabcd = AD² = 82² = 6724 кв. ед.