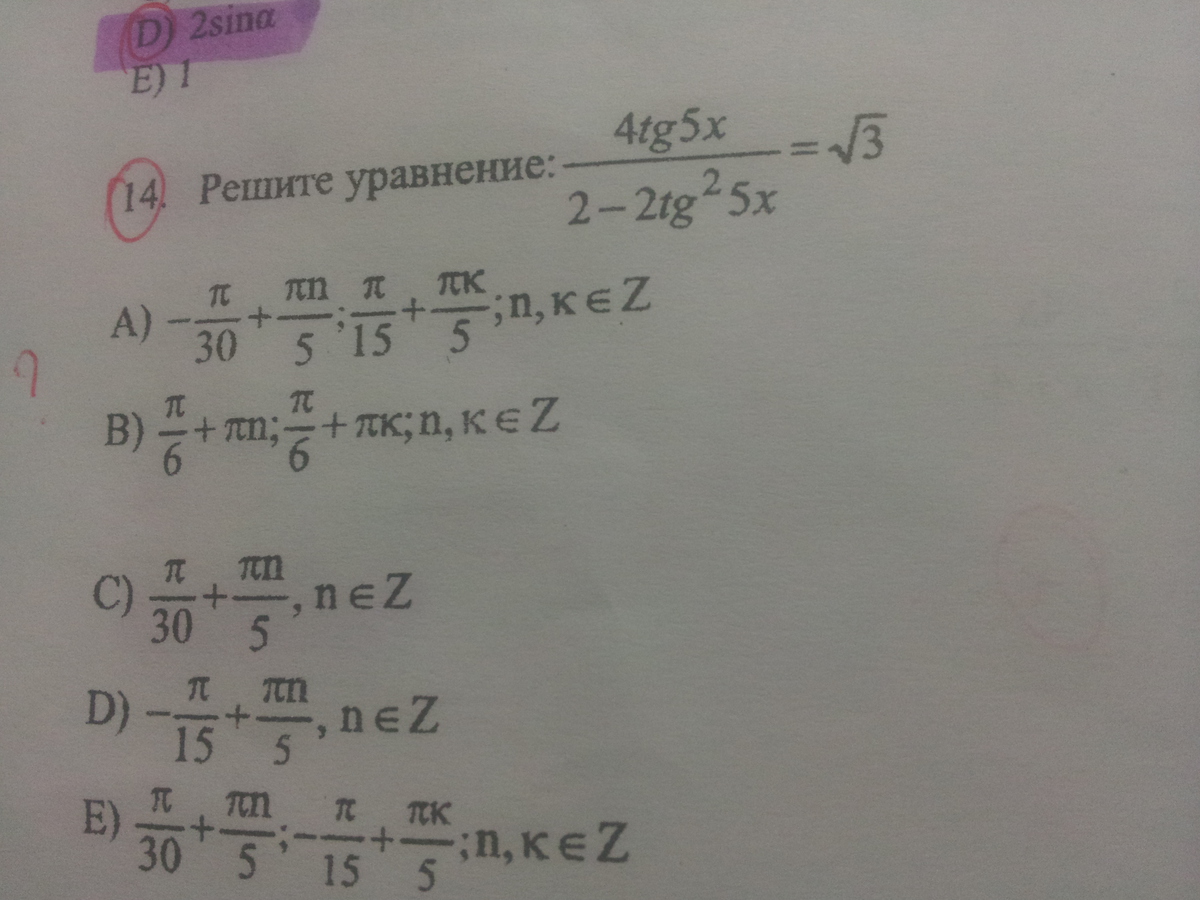Ответы
Ответ дал:
1
Ответ дал:
2
Одна из формул тригонометрии - тангенс двойного угла. Используем её в решении.

-----------------------------------------------------------------------------------------------

Ответ:
-----------------------------------------------------------------------------------------------
Ответ:
Вас заинтересует
2 года назад
2 года назад
2 года назад
7 лет назад
7 лет назад