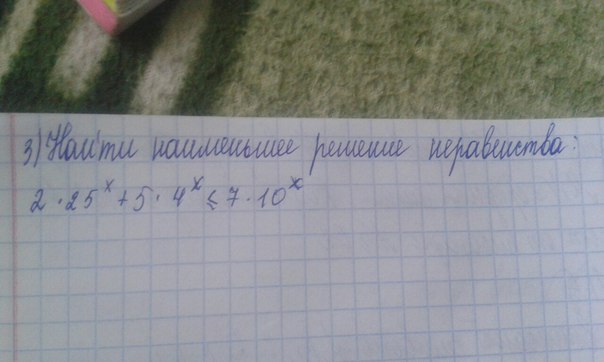Ответы
Ответ дал:
1
Легко
2*25^x + 5*4^x <= 7*10^x
2*(5^x)^2 - 7*5^x*2^x + 5*(2^x)^2 <= 0
Делим все на (2^x)^2
2*((5/2)^x)^2 - 7*(5/2)^x + 5 <= 0
Замена (5/2)^x = y > 0 при любом x
2y^2 - 7y + 5 <= 0
(y - 1)(2y - 5) <= 0
1 <= y <= 5/2
Обратная замена
1 <= (5/2)^x <= 5/2
0 <= x <= 1
Наименьшее решение, разумеется, равно 0.
2*25^x + 5*4^x <= 7*10^x
2*(5^x)^2 - 7*5^x*2^x + 5*(2^x)^2 <= 0
Делим все на (2^x)^2
2*((5/2)^x)^2 - 7*(5/2)^x + 5 <= 0
Замена (5/2)^x = y > 0 при любом x
2y^2 - 7y + 5 <= 0
(y - 1)(2y - 5) <= 0
1 <= y <= 5/2
Обратная замена
1 <= (5/2)^x <= 5/2
0 <= x <= 1
Наименьшее решение, разумеется, равно 0.
ialina061197:
спасибо большое) очень помогли)
Вас заинтересует
2 года назад
2 года назад
2 года назад
7 лет назад
9 лет назад