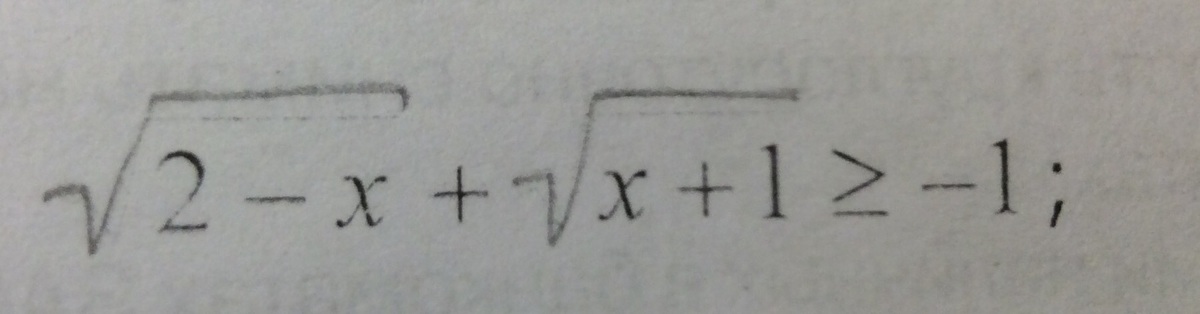Ответы
Ответ дал:
0
√(2-x)+√(x+1)≥0
ОДЗ 2-x≥0⇒x≤2 U x+1≥0⇒x≥-1
x∈[-1;2]
На данном промежутке сумма положительна или равна 0
Ответ x∈[-1;2]
ОДЗ 2-x≥0⇒x≤2 U x+1≥0⇒x≥-1
x∈[-1;2]
На данном промежутке сумма положительна или равна 0
Ответ x∈[-1;2]
Ответ дал:
0
Вас заинтересует
2 года назад
2 года назад
2 года назад
2 года назад
7 лет назад
9 лет назад