На прямой отмечены несколько точек так, что натуральные числа от 1 до 6 являются расстояниями между какими-то двумя отмеченными точками. Какое наименьшее количество точек может быть отмечено на прямой?
Матов:
перезагрузи страницу если не видно
Ответы
Ответ дал:
1
Если  включительно , то точек должно быть
включительно , то точек должно быть 

всего точек
точек
всего
Ответ дал:
3
Нужно 4 точки.
Расстояние BC = 2. CD = 3, DE = 1.
Тогда расстояние CE = 4, BD = 5, BE = 6.
Расстояние BC = 2. CD = 3, DE = 1.
Тогда расстояние CE = 4, BD = 5, BE = 6.
Приложения:
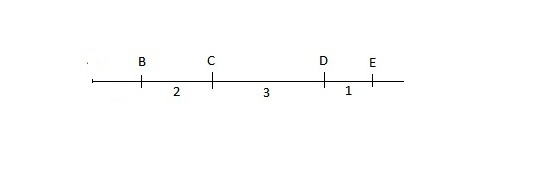
Все-таки 4 точки нужны)
А-В-С-D
AB = 2
AC = 5
AD = 6
Тогда CD = 1, BC = 3, BD = 4.
А-В-С-D
AB = 2
AC = 5
AD = 6
Тогда CD = 1, BC = 3, BD = 4.
Понял, исправил. Главное, у меня же был нарисован ответ, а я не сообразил.
Бывает)
Вас заинтересует
2 года назад
2 года назад
2 года назад
7 лет назад
9 лет назад
9 лет назад