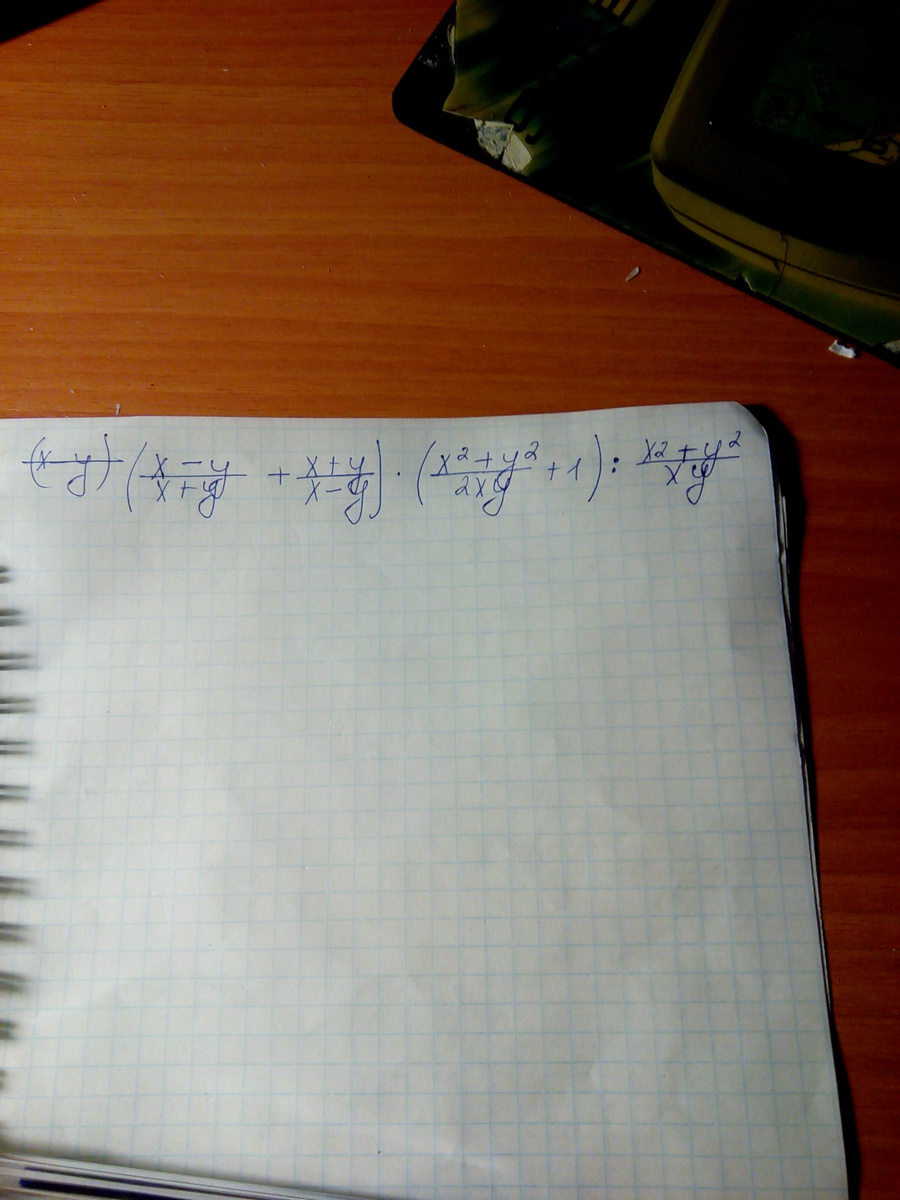Ответы
Ответ дал:
0
Если формулы не отобразятся (такое бывает на Android-устройствах), смотрите во вложении.
Приложения:
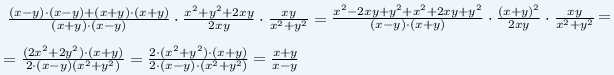
Ответ дал:
0
1)(x-y)/(x+y)+(x+y)/(x-y)=(x²-2xy+y²+x²+2xy+y²)/(x²-y²)=2(x²+y²)/(x²-y²)
2)(x²+y²)/2xy +1=(x²+y²+2xy)/2xy=(x+y)²/2xy
3)2(x²+y²)/(x²-y²) *(x+y)²/2xy=2(x²+y²)/(x-y)(x+y)*(x+y)²/2xy=(x²+y²)(x+y)/xy(x-y)
4)(x²+y²)(x+y)/xy(x-y) :(x²+y²)/xy=(x²+y²)(x+y)/xy(x-y) * xy/(x²+y²)=(x+y)/(x-y)
2)(x²+y²)/2xy +1=(x²+y²+2xy)/2xy=(x+y)²/2xy
3)2(x²+y²)/(x²-y²) *(x+y)²/2xy=2(x²+y²)/(x-y)(x+y)*(x+y)²/2xy=(x²+y²)(x+y)/xy(x-y)
4)(x²+y²)(x+y)/xy(x-y) :(x²+y²)/xy=(x²+y²)(x+y)/xy(x-y) * xy/(x²+y²)=(x+y)/(x-y)
Вас заинтересует
2 года назад
2 года назад
7 лет назад
7 лет назад
9 лет назад
9 лет назад