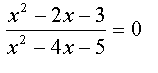Ответы
Ответ дал:
2
Аноним:
почему Вы числитель приравняли к нулю? это формула такая?
есть такое правило: если дробь равно 0 , то числитель равен нулю , а знаменатель не равен 0
есть такое понятие: область допустимых значений (ОДЗ). Если знаменатель равен нулю - дробь не определена (на ноль делить нельзя). приравнивая знаменатель к нулю мы находим те значения х которые не удовлетворяют ОДЗ. данные значения исключаются из полученных ранее.
Ясненько
Вас заинтересует
2 года назад
2 года назад
2 года назад
7 лет назад
7 лет назад
9 лет назад