c пункта А до окружности проведена касающая АВ и секучая которая проходит через центр окружности О и пересеекает ее у пунктах С и М(АС>АМ).известно что АВ=24,ОС=7.найдите длину отрезка АС
Ответы
Ответ дал:
0
см. рисунок.
вспоминаем сво-ва секущих, а также касательных. В данном случае
АС-секущая, МС-диаметр, АВ - касательная.
АМ*АС= AC=AM+2*7=AM+14
AC=AM+2*7=AM+14
AM*(AM+14)=

( -32 не подходит)
АС=18+14=32
вспоминаем сво-ва секущих, а также касательных. В данном случае
АС-секущая, МС-диаметр, АВ - касательная.
АМ*АС=
AM*(AM+14)=
( -32 не подходит)
АС=18+14=32
Приложения:
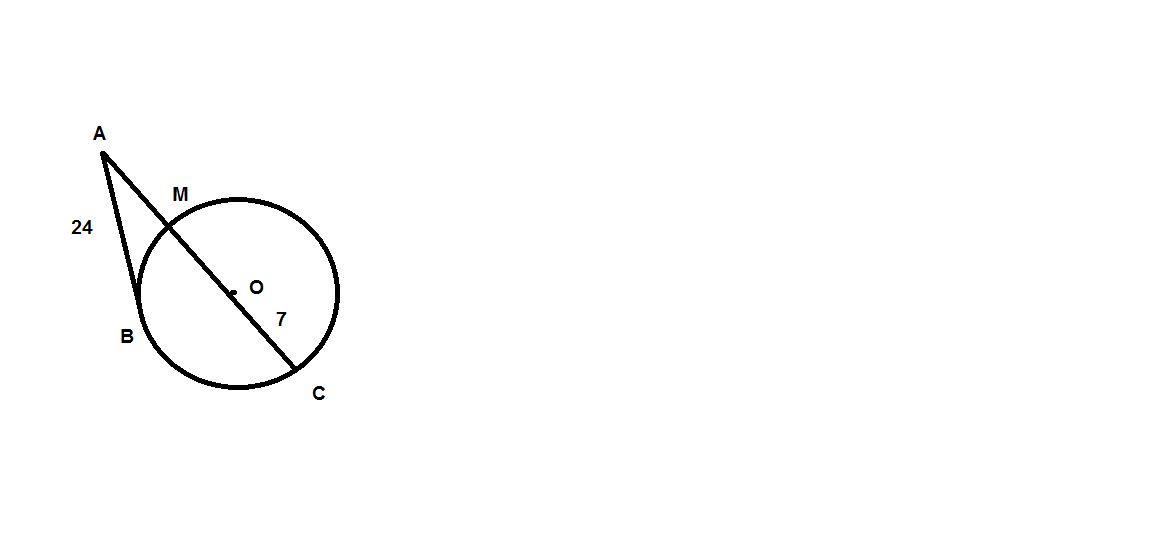
Аноним:
как всегда - чем мудрее, тем веселее!
Ответ дал:
0
ОС=ОВ - радиусы окружности;
ОВ перпендикулир к АВ (свойство радиуса проведенного к касательной окружности);
треугольник АВО - прямоугольный;
АВ=24, ОВ=7, АО=√(24²+7²)=25;
АС=АО+ОС=25+7=32.
ОВ перпендикулир к АВ (свойство радиуса проведенного к касательной окружности);
треугольник АВО - прямоугольный;
АВ=24, ОВ=7, АО=√(24²+7²)=25;
АС=АО+ОС=25+7=32.
отличное решение, можно и так. Вернее, так и нужно, как проще. Но многие просто забыли св-ва секущих-касательных, вот я и напомнил.
спасибо и на этом...
я всегда говорю правду , какая бы она ни была и от кого бы она ни шла. Правда- всегда правда. Так что ваше решение можно спокойно признавать лучшим, что ТС и сделает, надеюсь
Вас заинтересует
2 года назад
2 года назад
2 года назад
7 лет назад
7 лет назад