Помогите решить неравенство с логарифмами! Я понял что логарифмы нужно приравнять к общему основанию, но как тут это сделать.
Приложения:
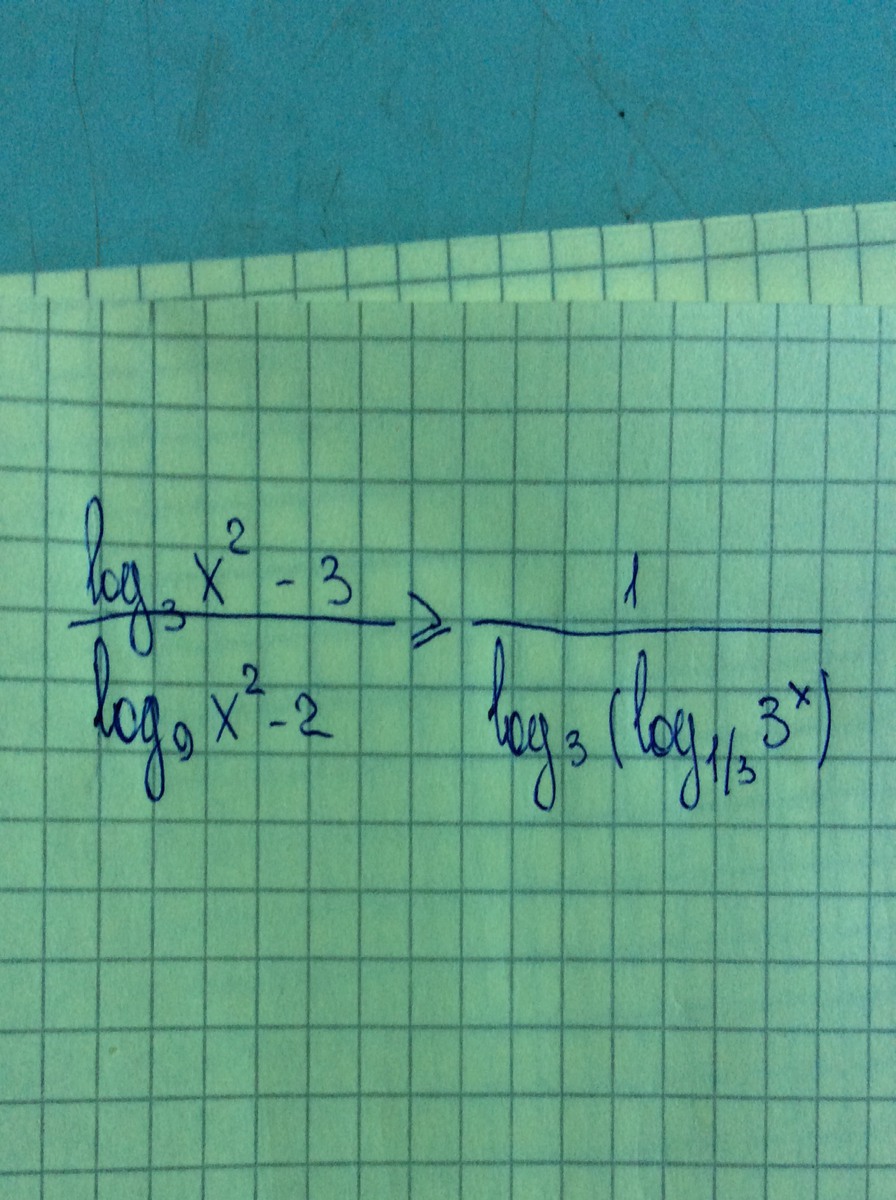
Ответы
Ответ дал:
0
Вас заинтересует
2 года назад
2 года назад
7 лет назад
7 лет назад
10 лет назад
10 лет назад
10 лет назад