Question

В правильной шестиугольной призме АВСDEFA₁В₁С₁D₁E₁F₁ все рёбра равны 5. Найдите расстояние от точки А до прямой С₁D₁

Answer 1

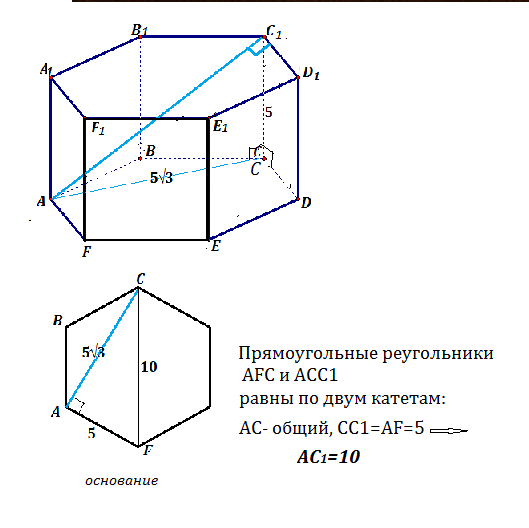
Искомое расстояние - перпендикуляр АС₁ из А к С₁D₁. 
СС₁- перпендикулярен плоскости основания призмы. . 
АС - проекция наклонной АС₁.
Соединим С и F, получим прямоугольный треугольник АСF. 
Правильный шестиугольник состоит из правильных треугольников. 
Угол ВСF=60°,  угол АСF=30°.
В треугольнике   АСF 
длина СF= длине 2-х рёбер =10  
Прямоугольные треугольники АСF и АСС1 равны по двум катетам. Следовательно, АС₁=СF=10.
------
Можно то же расстояние найти, вычислив длину АС ,  
АС=СF*sin 60°=5√3,  затем по т.Пифагора длину АС₁, но вряд ли есть  в этом необходимость.