7 класс. Помогите пожалуйста :с
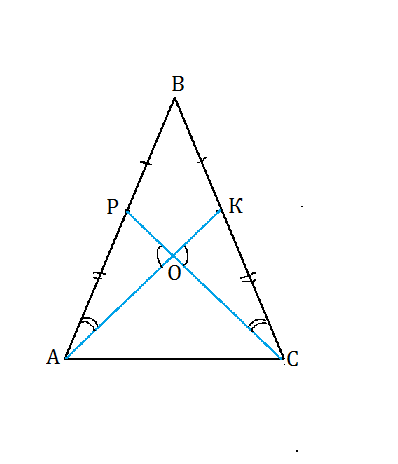
Треугольник ABC равнобедренный с основанием AC. На сторонах AB и BC отмечены точки P и K так, что BP=BK. O- точка пересечения AK и CP. Докажите,что треугольник AOC равнобедренный.
Ответы
Ответ дал:
0
Для 7 класса выгодней,конечно,способ 2(простой)
Приложения:

Ответ дал:
0
Рассмотрим треугольники АВК и СВР. Они равны по двум сторонам и общему углу В между ними. ⇒
∠ ВАК =∠ ВСР.
Т.к. АВ=ВС, и ВР=ВК, то равны и другие части этих сторон: АВ=СК.
В треуголькиках АОР и СОК углы РОА и КОС равны как вертикальные, а
∠КСО=∠ВАО (из вышесказанного), следовательно, равны в них и
∠АРО и ∠СКО.
В треугольниках АОР и СОК имеется по равной стороне (АР=СК) и по двум прилежащим к ним углам. ⇒эти треугольники равны, и в треугольнике АОС стороны
АО=ОС. Треугольник, в котором две стороны равны, - равнобедренный, что и требовалось доказать.
∠ ВАК =∠ ВСР.
Т.к. АВ=ВС, и ВР=ВК, то равны и другие части этих сторон: АВ=СК.
В треуголькиках АОР и СОК углы РОА и КОС равны как вертикальные, а
∠КСО=∠ВАО (из вышесказанного), следовательно, равны в них и
∠АРО и ∠СКО.
В треугольниках АОР и СОК имеется по равной стороне (АР=СК) и по двум прилежащим к ним углам. ⇒эти треугольники равны, и в треугольнике АОС стороны
АО=ОС. Треугольник, в котором две стороны равны, - равнобедренный, что и требовалось доказать.
Приложения:
Вас заинтересует
2 года назад
8 лет назад
8 лет назад
10 лет назад
10 лет назад