Question

В правильной треугольной пирамиде ABCD с основанием ABC известны ребра: AB=12√3, SC=13. Найдите угол, образованный плоскостью основания и прямой, проходящей через середины ребер AS и BC. В ответ напишите котангенс этого угла.

Answer 1

Ответ на эту задачу уже давался

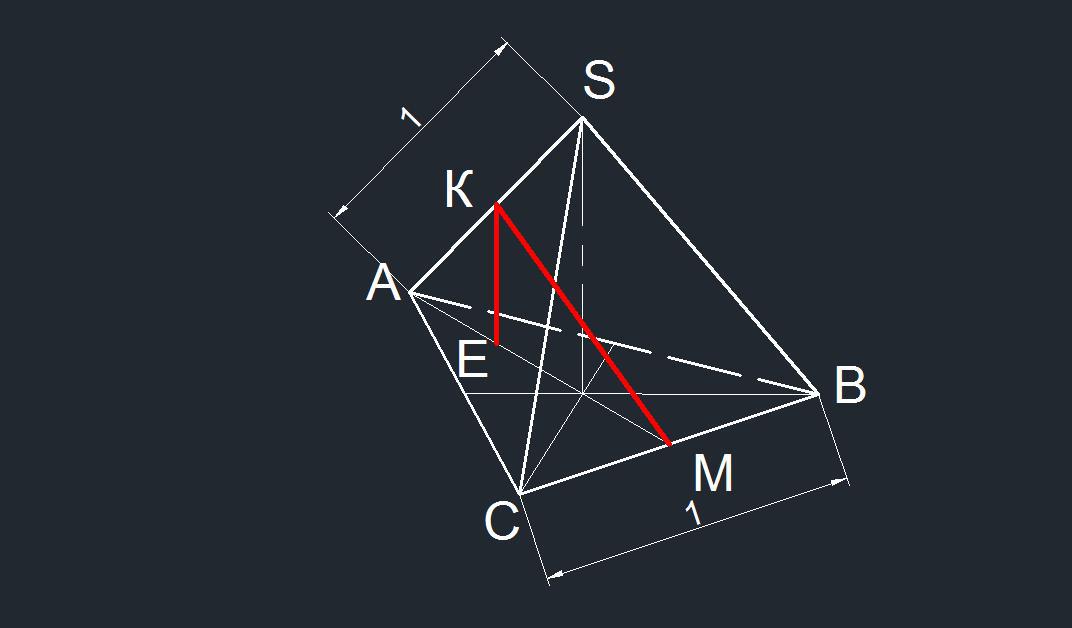
Отрезок прямой, проходящей через середины ребер AS и BC, обозначим КМ.
Медиана основания АМ (она же и высота и биссектриса основания) равна АВ*cos 30° = 12√3 * (√3/2) = 18.
Точка К на середине ребра SA проецируется на медиану в точку Е, находящуюся посредине отрезка АО, равного 2/3 АМ.
АО = (2/3)*18 = 12, ЕО = (1/2)*12 = 6.
Отсюда ЕМ = 6+(1/3)*18 = 6 + 6 = 12.
Высота пирамиды SO = √(SA²-AO²) = √(13²-12²) = √(169-144) = √25 = 5.
Отрезок КЕ равен половине высоты пирамиды: КЕ = 5/2 = 2,5.
Угол, образованный плоскостью основания и прямой, проходящей через середины ребер AS и BC, - это угол КМЕ = α.
ctg α = EM / KE = 12 / 2.5 = 4.8.
α = arc ctg 4.8 =  0.205395 радиан = 11.76829 градуса 

Answer 2

Большое спасибо,я пробовал методой координат и к сажалению мне не получилось