Question

8й класс, параллелограмм!Помогите пожалуйста!! 9ю и 10ю

Answer 1

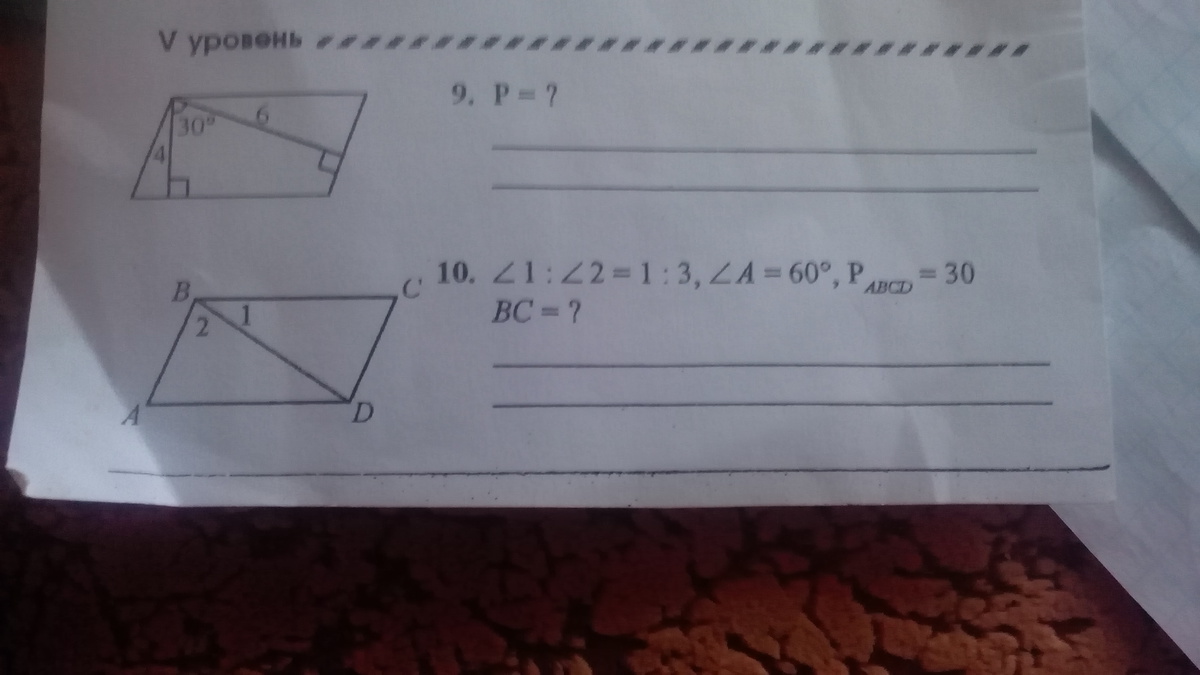
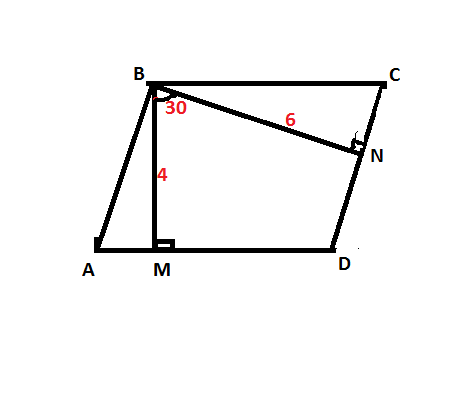
9. ABCD - параллелограмм
BК=4, ВК_|_AD
 BM=6, BM_|_CD
<KBM=30° <D=360°-(30°+90°+90°), <D=150° => <A=30°
ΔAKB: AB=4*2, AB=8 (катет против угла в 30° в 2 раза меньше гипотенузы)
ΔВМС: <C=30°, >BMC=90°, ⇒BC=6*2, BC=12
PABCD=2*(8+12)=40
PABCD=40

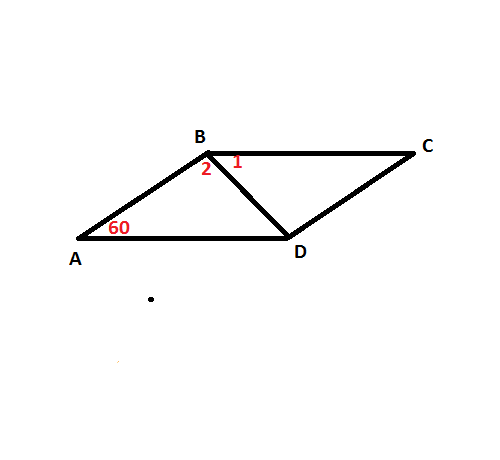
10. <A=60°, <B=180°-60°, <B=120°. 
<B=<1+<2, <!=1*x, <2=3*x
x+3x=120, 4x=120°, x=30°
ΔABD:<A=60°, <ABD=90°, <ADB=30°⇒
AD=2*AB (катет против угла 30°)
AB=y,AD=2y
P=2*(y+2y)
30=6y, y=5
BC=10

Answer 2

9. В четырехугольнике MBND сумма углов равна 360
<MDN(или<ADC) = 360 - 90 - 90 - 30 = 150
<BAD и <ACD - односторонние углы, их сумма равна 180
<BAD = 180 - 150 = 30
Рассм. ΔABM - прямоугольный, AB = BM/sin 30 = 4/ 1/2 = 4 * 2 = 8
<BAD = <BCD = 30 - как противоположные углы параллелограмма, 
Рассм. ΔBCD - прямоугольный, BC = BN/sin30 = 6/ 1/2 = 12
P(ABCD) = 2AB + 2BC = 2 *8 + 2*12 = 16 + 24= 30
10.<BAC и <ABC - односторонние углы, их сумма равна 180
<ABC = 180 - 60 = 120
<ABD = 120/4 * 3= 90
Рассм. ΔABD - прямоугольный, <ADB = 90 - 60 = 30, из этого следует, что АB = 1/2 AD или AB = 1/2 BC (AD = BC)
P(ABCD) = 2AB + 2BC = 2(AB + BC) =30
BC = 30/2 - AB = 15 - AB
BC = 2AB 
2AB = 15 - AB
3AB = 15
AB = 5
BC = 2*5 = 10