Помогите решить, нужно разложить на множители. Ответ должен получиться (a+b)(a-4b).
И напишите пожалуйста решение.
Приложения:
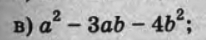
Ответы
Ответ дал:
0
-3ab=-4ab+ab
a²-3ab-4b²=a²+ab-4ab-4b²=(a²+ab)-(4ab+4b²)=a*(a+b)-4b(a+b)=(a+b)*(a-4b)
a²-3ab-4b²=
пусть а -переменная, b -постоянная.
раскладываем на множители квадратный трехчлен:
a²-3ab-4b²=(a-a₁)*(a-a₂)
D=(-3b)²-4*(-4b)=25b²
a₁=(3b+5b)/2=4b
a₂=(3b-5b)/2=-b
a²-3ab-4b²=(a-4b)*(a+b)
a²-3ab-4b²=a²+ab-4ab-4b²=(a²+ab)-(4ab+4b²)=a*(a+b)-4b(a+b)=(a+b)*(a-4b)
a²-3ab-4b²=
пусть а -переменная, b -постоянная.
раскладываем на множители квадратный трехчлен:
a²-3ab-4b²=(a-a₁)*(a-a₂)
D=(-3b)²-4*(-4b)=25b²
a₁=(3b+5b)/2=4b
a₂=(3b-5b)/2=-b
a²-3ab-4b²=(a-4b)*(a+b)
Ответ дал:
0
А можно это как-то решить через выделение полного квадрата?
Ответ дал:
0
a² - 3 ab - 4 b² = a² - 3b * a - 4b²
Решим a² - 3b * a - 4b² = 0 как квадратное уравнение относительно а,
где
1 - первый коэффициент
3b - второй коэффициент
(- 4b²) - свободный член
Ищем D - дискриминант
D = (3b)² - 4 * 1 * (- 4b²) = 9b² + 16b² = 25b²
√D = √(25b²) = 5b
a₁ = (3b + 5b)/2 = 8b/2 = 4b
a₂ = (3b - 5b)/2 = - 2b/2 = - b
a² - 3 ab - 4 b² = (a - 4b) * ((a - (- b)) = (a - 4b) * (a + b)
Решим a² - 3b * a - 4b² = 0 как квадратное уравнение относительно а,
где
1 - первый коэффициент
3b - второй коэффициент
(- 4b²) - свободный член
Ищем D - дискриминант
D = (3b)² - 4 * 1 * (- 4b²) = 9b² + 16b² = 25b²
√D = √(25b²) = 5b
a₁ = (3b + 5b)/2 = 8b/2 = 4b
a₂ = (3b - 5b)/2 = - 2b/2 = - b
a² - 3 ab - 4 b² = (a - 4b) * ((a - (- b)) = (a - 4b) * (a + b)
Вас заинтересует
2 года назад
2 года назад
8 лет назад
8 лет назад
10 лет назад
10 лет назад