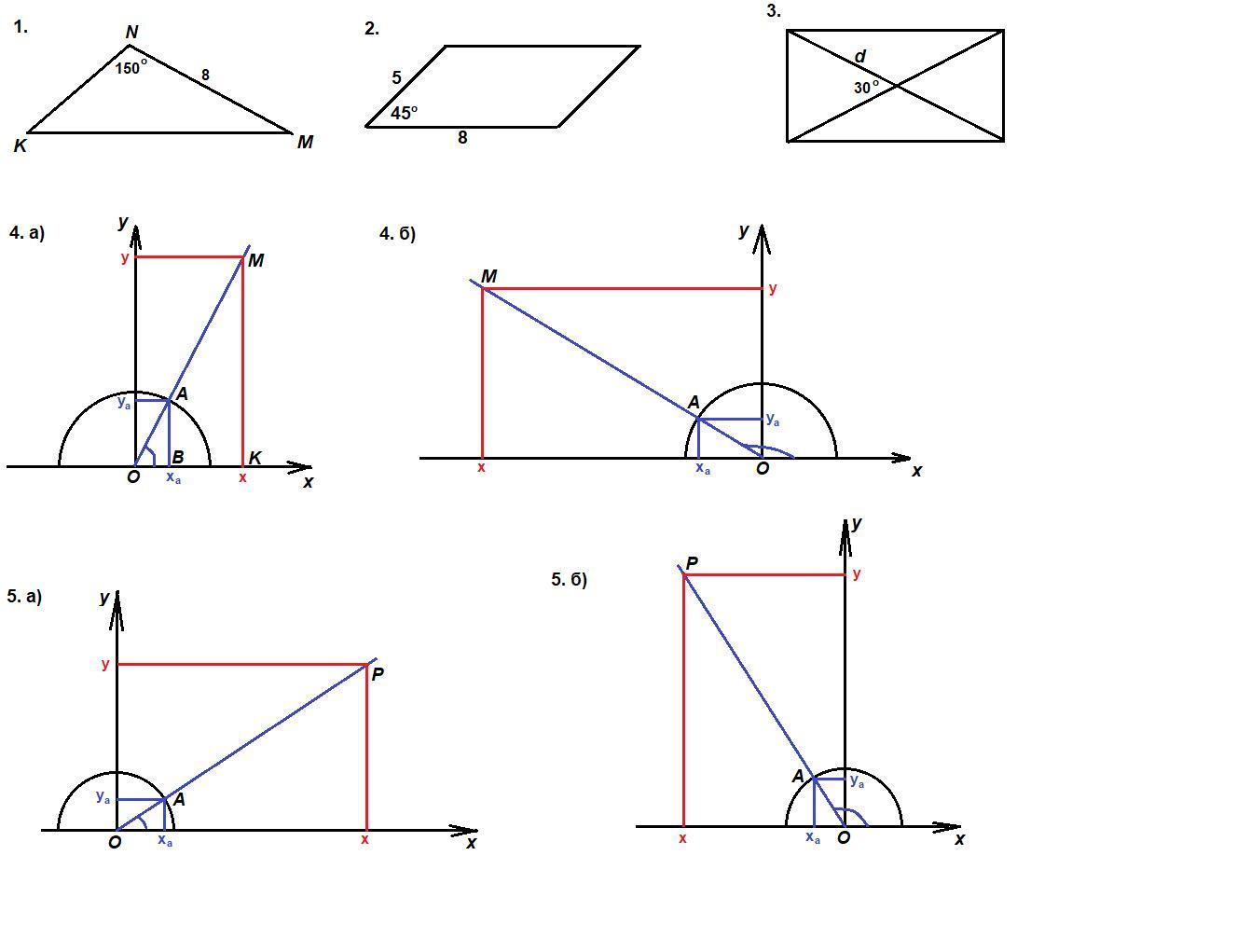
1. В треугольнике MNK уголMNK = 150°, MN = 8, а площадь тре¬угольника равна 20. Найдите NK.
2. В параллелограмме один из углов равен 45°, а его стороны равны 5 см и 8 см. Найдите его площадь.
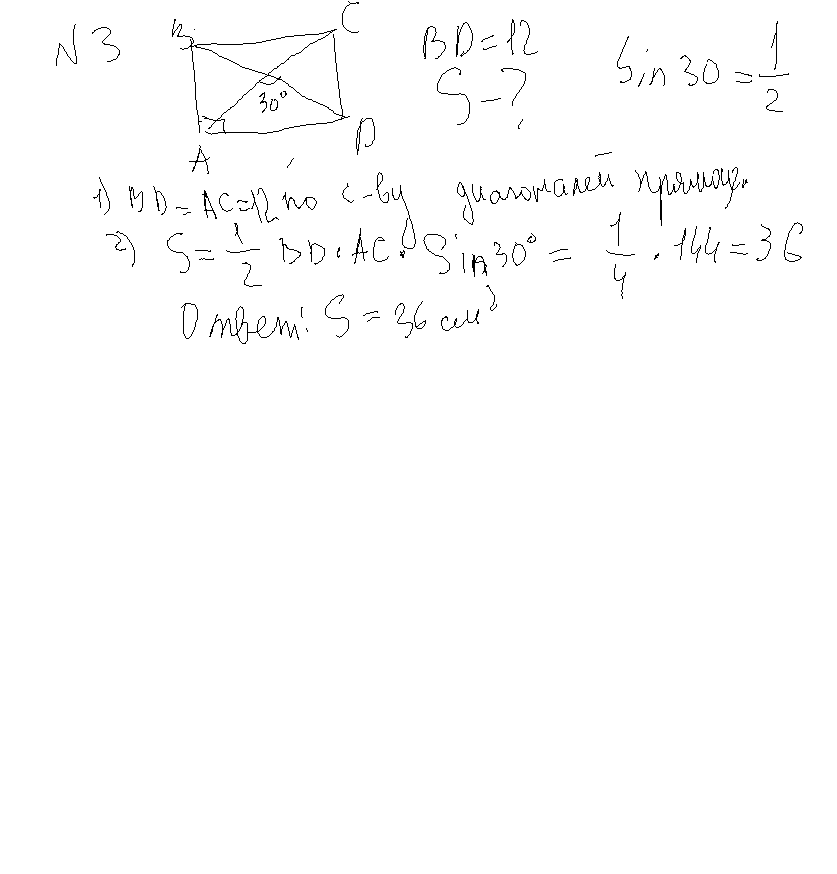
3. В прямоугольнике диагональ равна 12 см, а угол между диагоналями 30°. Найдите площадь прямоугольника.
4.Угол между лучом ОМ, пересекающим единичную полуокружность, и положительной полуосью Ох равен а. Найдите координаты точки М, если: а) ОМ = 4; a = 60°; б) ОМ= 8; а= 150°.
5.Угол между лучом ОР, пересекающим единичную полуокружность, и положительной полуосью Ох равен р. Найдите координаты точки Р, если: а) ОР = 6; р = 30°; б) ОР= 10; р = 120°
Ответы
1 и 2.. сейчас ещё 3 напишу
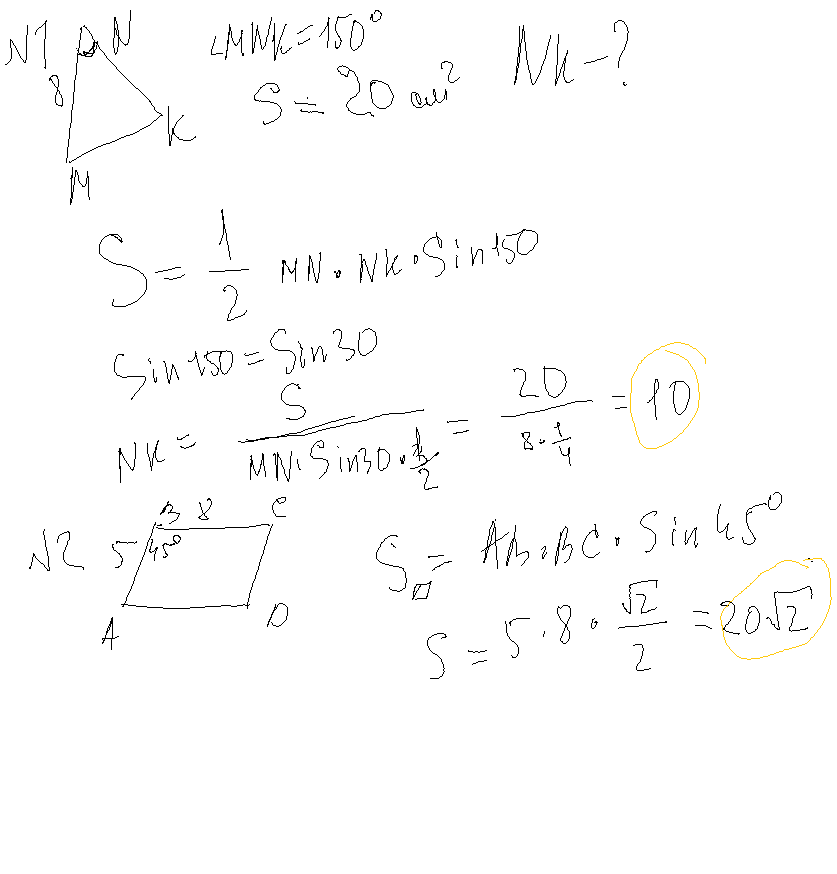
Ответ:
1. 10
2. 20√2 см²
3. 36 см²
4. а) (2; 2√3)
б) (- 4√3; 4)
5. а) (3√3; 3)
б) (- 5; 5√3)
Объяснение:
1.
Площадь треугольника равна половине произведения двух его сторон на синус угла между ними:
Smnk = 1/2 · MN · NK · sin∠MNK
sin∠MNK = sin 150° = sin (180° - 30°) = sin 30° = 1/2
20 = 1/2 · 8 · NK · 1/2
20 = 2 · NK
NK = 20 / 2 = 10
2.
Площадь параллелограмма равна произведению его смежных сторон на синус угла между ними.
S = 5 · 8 · sin 45° = 40 · √2/2 = 20√2 см²
3.
Площадь любого четырехугольника можно найти как половину произведения диагоналей на синус угла между ними.
Диагонали прямоугольника равны.
S = 1/2 d² · sin 30° = 1/2 · 12² · 1/2 = 36 см²
4.
а) А - точка пересечения луча ОМ с единичной окружностью.
Координаты точки А:
xₐ = cos 60° = 1/2
yₐ = sin 60° = √3/2
ΔOAB подобен ΔOMK по двум углам (угол О общий, ∠В = ∠К = 90°), ⇒
x : xₐ = OM : OA
x = xₐ · OM = 1/2 · 4 = 2
Аналогично,
y = yₐ · OM = √3/2 · 4 = 2√3
б) xₐ = cos 150° = cos (180° - 30°) = - cos 30° = - √3/2
yₐ = sin 150° = sin (180° - 30°) = sin 30° = 1/2
x = xₐ · OM = - √3/2 · 8 = - 4√3
y = yₐ · OM = 1/2 · 8 = 4
5.
а) xₐ = cos 30° = √3/2
yₐ = sin 30° = 1/2
x = xₐ · OР = √3/2 · 6 = 3√3
y = yₐ · OP = 1/2 · 6 = 3
б) xₐ = cos 120° = cos (180° - 60°) = - cos 60° = - 1/2
yₐ = sin 120° = sin (180° - 60°) = sin 60° = √3/2
x = xₐ · OP = - 1/2 · 10 = - 5
y = yₐ · OP = √3/2 · 10 = 5√3