Question

Квадрат АВСD и АВС1D1 лежат в плоскостях, угол между которыми равен 60 градусов. Найдите расстояние между их центрами, если AB=a.
Решите и нарисуйте рисунок к этой задаче
Ответ должен получится 0,5а

Answer 1

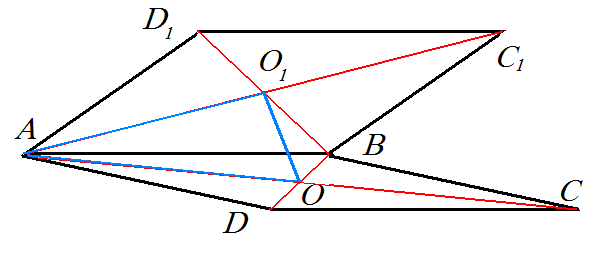
Дано:
квадрат ABCD = квадрат ABC₁D₁
AB = a
AC = AC₁ = d 
угол DAD₁ = угол CAC₁ = 60°
Найти: OO₁

Решение:
По формуле диагонали квадрата
$d = AC=a sqrt{2}$  ⇒ 
⇒ AO = AO₁ = $frac{1}{2} * asqrt{2}$  = $frac{ sqrt{2} }{2} *a = frac{1}{2}a$ ⇒
⇒ ΔO₁AO - равнобедренный
Так как угол O₁AO = 60°, а по сумме углов 180 - 60 = 120°, то другие два угла OO₁A = O₁OA = 120/2 = 60°. Следовательно ΔO₁AO - равносторонний O₁A = AO = OO₁ = $frac{1}{2}a$
Ответ: расстояние между центрами равно  $frac{1}{2}a$