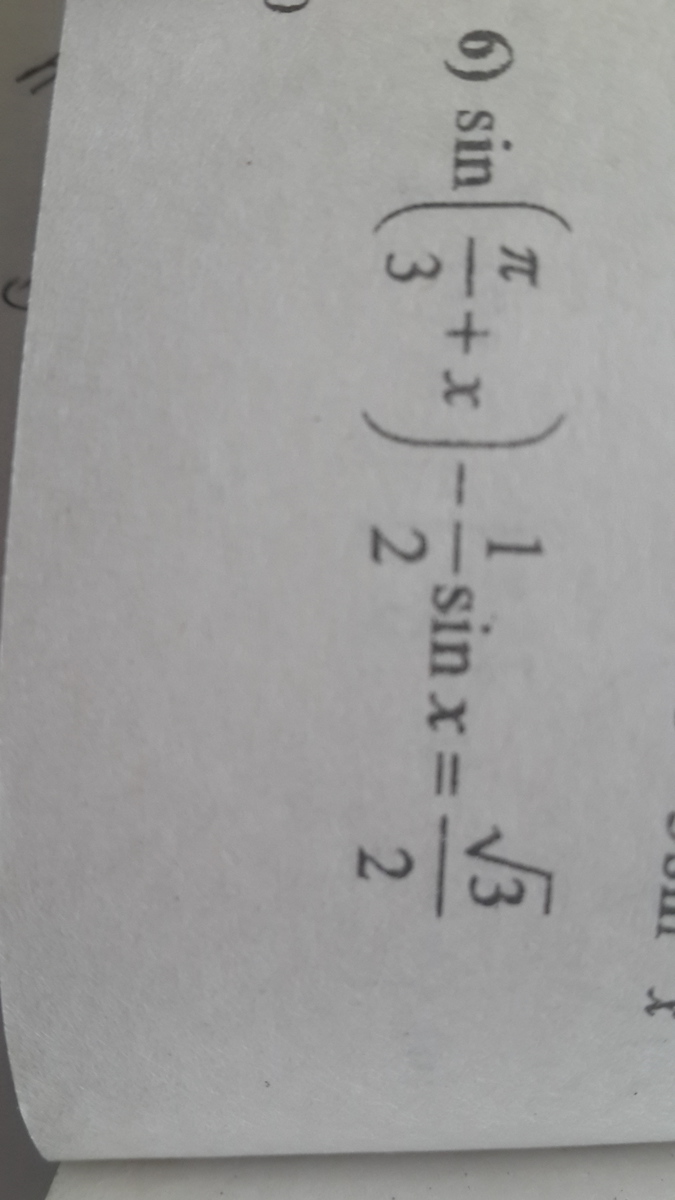Ответы
Ответ дал:
0
sin(π/3+x)-(1/2)*sinx=√3/2
Используем формулу синус суммы sin(α+β)=sinαcosβ+cosαsinβ:
sin(π/3)*cosx+cos(π/3)*sinx-(1/2)*sinx=√3/2
(√3/2)*cosx+(1/2)*sinx-(1/2)*sinx=√3/2
(√3/2)*cosx=√3/2
cosx=1
x=2πn, n∈Z.
Используем формулу синус суммы sin(α+β)=sinαcosβ+cosαsinβ:
sin(π/3)*cosx+cos(π/3)*sinx-(1/2)*sinx=√3/2
(√3/2)*cosx+(1/2)*sinx-(1/2)*sinx=√3/2
(√3/2)*cosx=√3/2
cosx=1
x=2πn, n∈Z.
Вас заинтересует
2 года назад
7 лет назад
7 лет назад
10 лет назад