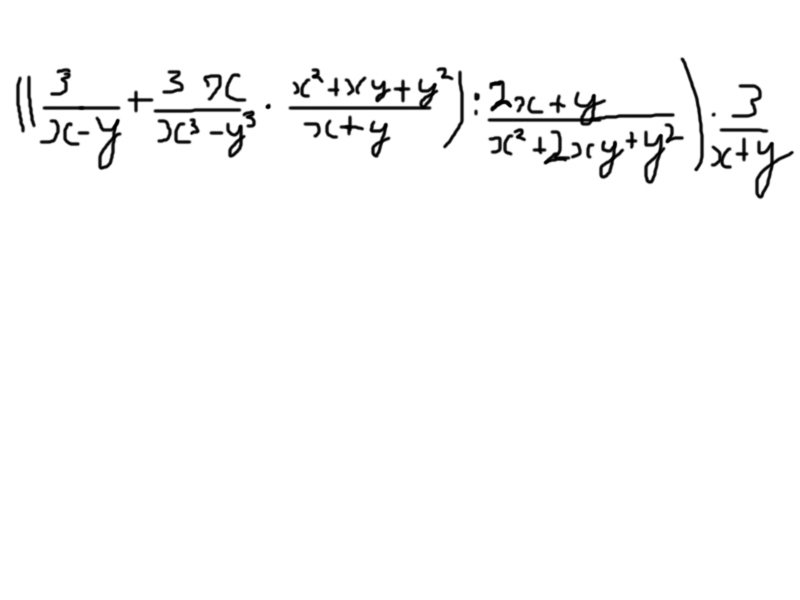Ответы
Ответ дал:
0
Ответ дал:
0
не очень понятно)
Ответ дал:
0
что именно непонятно?
Ответ дал:
0
Основная мысль такая: там где не хватает множителя, чтобы получилась полная формула сокращённого умножения, добавляем этот множитель. А чтобы дробь не изменилась, умножаем на него и числитель и знаменатель.
Вас заинтересует
2 года назад
2 года назад
8 лет назад
10 лет назад
10 лет назад
10 лет назад