Question

помогите пожалуйста.

Answer 1

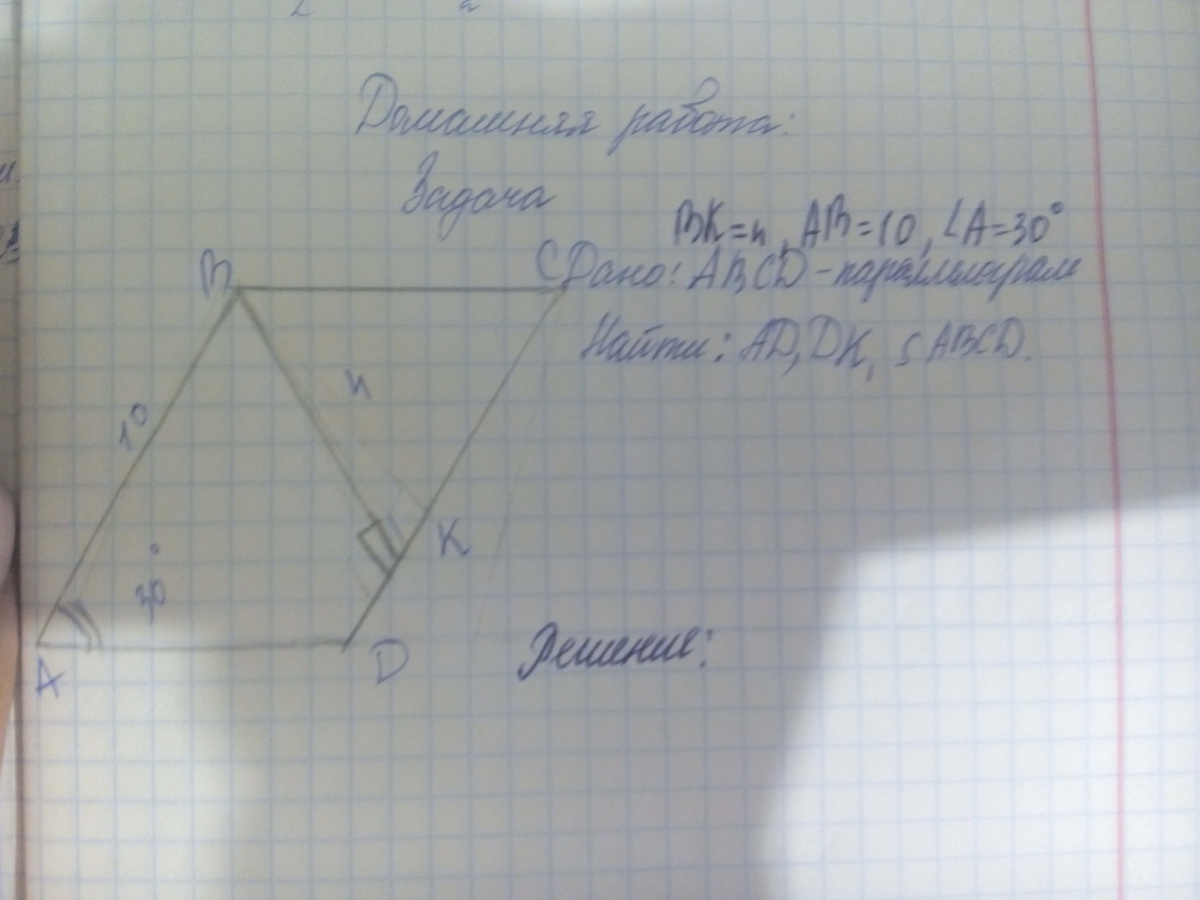
Если отрезок ВК перпендикулярен CD и равен n, то решение:
<C=<A=30°, как противоположные углы параллелограмма.
Тогда в прямоугольном треугольнике КВС (<CKB=90°) катет ВК лежит против угла 30°, поэтому гипотенуза ВС=2n. Тогда катет СК=√(4n²-n²)=n√3.
DK=CD-CK=10-n√3.
AD=BC=2n (как противоположные стороны параллелограмма).
Sabcd=BK*AD=10n. (Площадь параллелограмма равна произведению его стороны на высоту, опушенную на эту сторону.
Ответ: AD=2n, DK=10-n√3, Sabcd=10n.