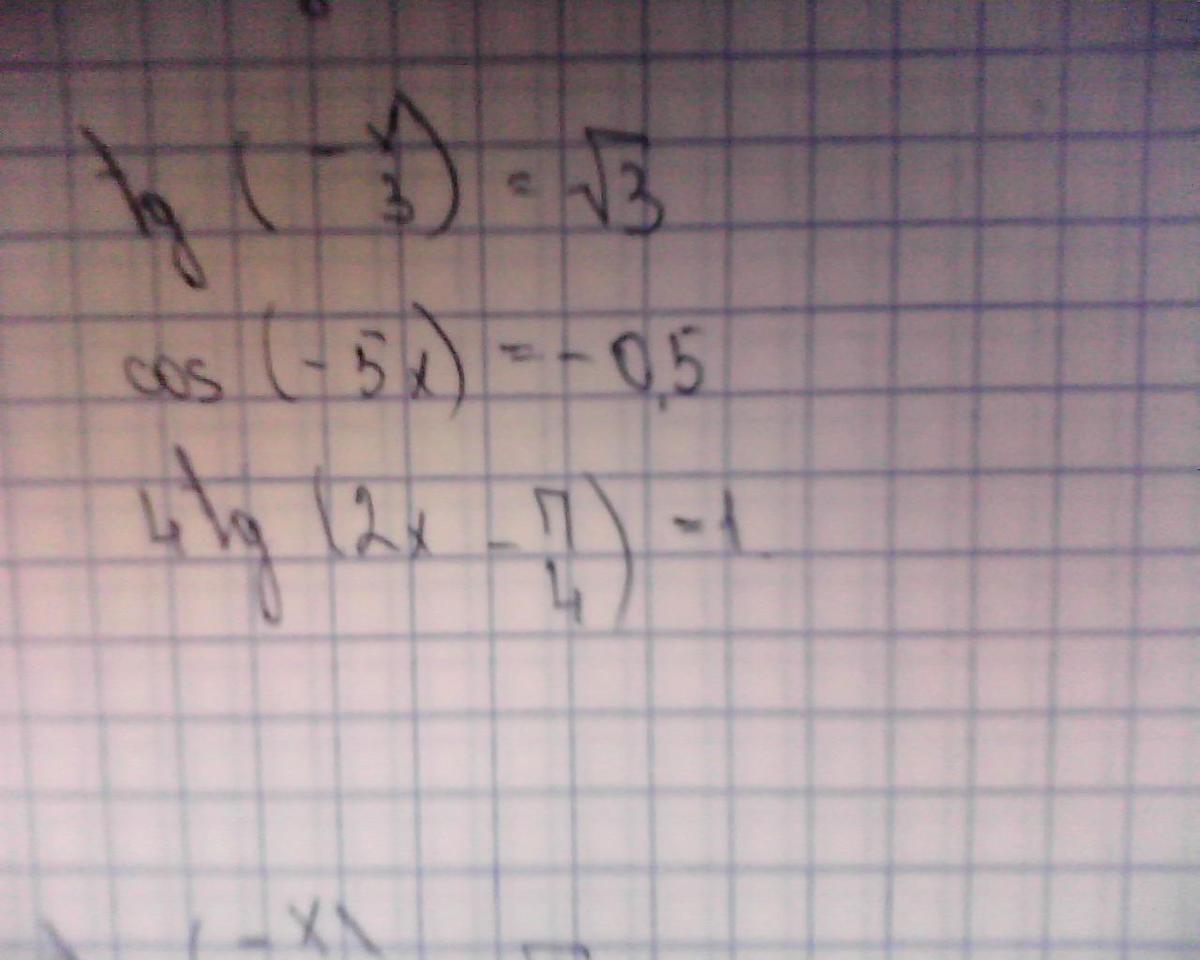Ответы
Ответ дал:
0
Так как тангенс- нечетная функция, то


Так как косинус- четная функция, то



Так как косинус- четная функция, то
Ответ дал:
0
большое спасибо за качественную и своевременную помощь)
Ответ дал:
0
спасибо и Вам
Вас заинтересует
2 года назад
2 года назад
8 лет назад
10 лет назад
10 лет назад