Question

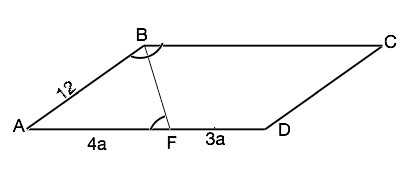
В параллелограмме ABCD биссектриса угла B пересекает сторону AD в точке F. Найдите периметр параллелограмма если AB = 12, AF:FD=4:3

Answer 1

     Биссектриса угла параллелограмма отсекает от него равнобедренный треугольник ( угол при В делится пополам, а углы ∠AFB=∠CBF - накрестлежащие, поэтому углы при ВF равны и АF=AB). Примем коэффициент отношения AF:FD равным а. Тогда AF=4a, FD=3a Из равенства АF=AB находим а=12:4=3. ⇒ FD=3•3=9.⇒ AD=12+9=21. Противоположные стороны параллелограмма равны. Р(АВСD)=2•(21+12)=66 (ед. длины).